Cтандартизация данных
Содержание
Cтандартизация данных¶
Приёмы стандартизации данных:
Логарифмирование
Нормализация
Логарифмирование данных¶
Рассмотрим один из наборов данных, идущих с пакетом R (описание), который содержит подсчеты числа видов млекопитающих на разных островах в Юго-Восточной Азии.
Name Название острова
Area Площадь (км2)
Species Количество видов млекопитающих
logArea логарифм Area
logSpecies логарифм Species
Первоисточник
Heaney, Lawrence R. (1984) Mammalian species richness on islands on the Sunda Shelf, Southeast Asia, Oecologia.
D = pd.read_csv('d/SpeciesArea.csv', index_col=0)
D
| Name | Area | Species | logArea | logSpecies | |
|---|---|---|---|---|---|
| 1 | Borneo | 743244 | 129 | 13.51880 | 4.85981 |
| 2 | Sumatra | 473607 | 126 | 13.06810 | 4.83628 |
| 3 | Java | 125628 | 78 | 11.74110 | 4.35671 |
| 4 | Bangka | 11964 | 38 | 9.38966 | 3.63759 |
| 5 | Bunguran | 1594 | 24 | 7.37400 | 3.17805 |
| 6 | Banggi | 450 | 18 | 6.10925 | 2.89037 |
| 7 | Jemaja | 194 | 15 | 5.26786 | 2.70805 |
| 8 | Karimata Besar | 130 | 19 | 4.86753 | 2.94444 |
| 9 | Tioman | 114 | 23 | 4.73620 | 3.13549 |
| 10 | Siantan | 113 | 16 | 4.72739 | 2.77259 |
| 11 | Sirhassan | 46 | 16 | 3.82864 | 2.77259 |
| 12 | Redang | 25 | 8 | 3.21888 | 2.07944 |
| 13 | Penebangan | 13 | 13 | 2.56495 | 2.56495 |
| 14 | Perhentian Besar | 8 | 6 | 2.07944 | 1.79176 |
Посмотрим распределение значений.
sns.regplot(x='Area', y='Species', data=D, fit_reg=False);
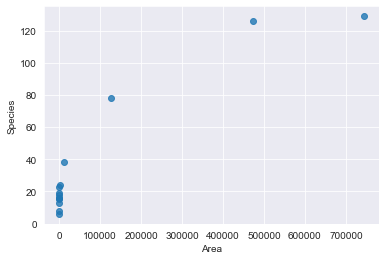
Мы видим прямую зависимость: больше площадь - больше видов. При этом график функции замедляет свой рост при высоких значениях площади.
Чтобы нагляднее отобразить зависимость используются логарифмическая шкала. В данном наборе данных прологарифмированные значения уже включены в набор.
sns.regplot(x='logArea', y='logSpecies', data=D);
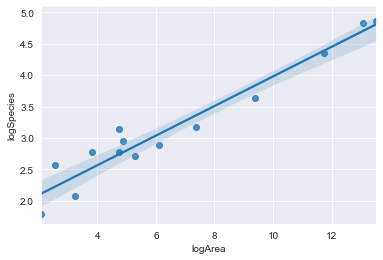
В логарифмической шкале облако точек выглядит более равномерным. Точки для крупных островов стали ближе друг к другу, а точки для мелких можно отличить друг от друга.
Логарифмирование помогает тогда, когда в одном наборе данных мы хотим охватить большой диапазон значений, различающихся на порядок и более. Широко известные примеры: показатель кислотности воды pH, громкость звука над порогом слышимости дБ.
Логарифмированные данные в таблице получены логарифмом с основанием \(e\). Логарифмирование позволяет получить более равномерное распределение. Такой же паттерн точек можно получить, если данные не преобразовывать, а только менять шкалу по обеим осям. Обратите внимание на отображение подписей к обеим шкалам.
axes().set(xscale="log", yscale="log")
sns.regplot(x='Area', y='Species', data=D, fit_reg=False);
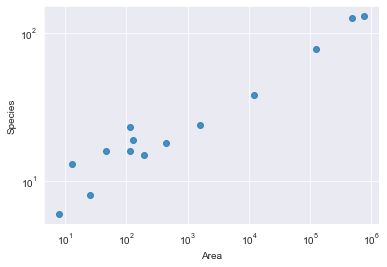
Чтобы рассчитать линейную модель логарифмов данных, их нужно преобразовать до построения рисунка.
sns.regplot(D.Area.apply(log), D['Species'].apply(log), data=D, fit_reg=True);
title('Логарифмированные данные с основанием 2.71');
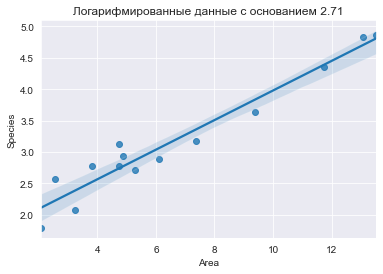
Логарифмирование с другим основанием дает другие значения (см. на оси), но такой же паттерн точек.
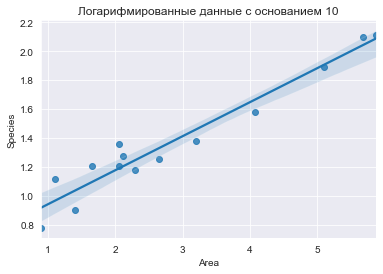
sns.regplot(D.Area.apply(log10), D['Species'].apply(log10));
title('Логарифмированные данные с основанием 10');
См.также
Википедия знает о кривой «вид-площадь».
