Генератор случайных чисел
Содержание
Генератор случайных чисел¶
Рассмотрим результаты вызова функции normal() с параметром size больше 1.
x = normal(size=40)
x
array([-0.46820879, -0.82282485, -0.0653801 , -0.71336192, 0.90635089,
0.76623673, 0.82605407, -1.32368279, -1.75244452, 1.00244907,
0.54480945, 1.8951609 , -0.76935745, -1.40309592, -0.63246751,
-0.55887367, -1.23323138, -0.43950352, 0.91478726, 0.26504093,
-1.38337015, 0.6855118 , 0.45609091, -0.46137426, 0.0947003 ,
-1.54281161, 2.4793696 , 0.45686676, -0.31387278, 0.02103738,
0.96079316, 0.0584829 , -0.44603217, 0.31919714, 0.84116862,
-1.53276199, -0.28158426, 1.74445271, -0.67423891, 0.58840123])
Возвращаемый массив чисел включает положительные и отрицательные числа, самое маленькое из которых около -2, а самое большое - около +2.
Для удобства восприятия будем выводить числа в созданном массиве в виде рисунка. Замените последнюю строку в блоке кода на команду построения рисунка
plot(x, 'o');. Таким образом, при выполнении кода ячейки мы будем создавать массив чисел и тут же отображать его на рисунке. Для многократного выполнения кода ячейки нажимайтеCtrl-Enter.
Команда plot() (англ. чертеж) рисует график по заданным координатам.
Если на вход функции подать только один массив чисел, то по горизонтальной оси откладывается их порядковый номер, а их собственные значения откладываются по вертикали.
Второй параметр функции - это формат графика, буква 'o' означает круглые точки без соединительной линии между ними.
plot(x, 'o');
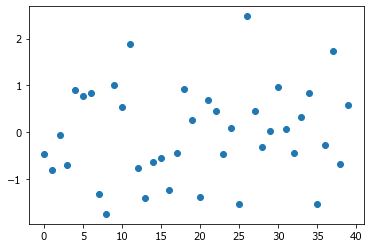
Попробуйте увеличить размер выборки (например, 400, 4000).
x = normal(size=4000)
plot(x, 'o');

При большом количестве исходов видно, что случайная нормальная выборка представляет собой массив положительных и отрицательных чисел в диапазоне от -3 до 3. Очень редко встречаются числа с удалением на 4 и более единиц, большинство значений заполняют диапазон между -2 и 2.
Для наглядного представления построим гистограмму распределения.
hist(x, bins=40);
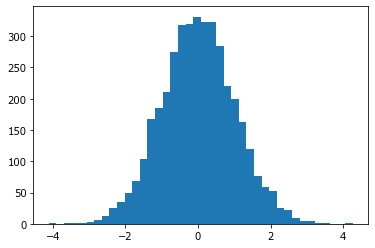
Для генератора выборки из нормального распределения можно задать два параметра - loc (локализацию) и scale (шкалу, размах). Локализация сдвигает центр распределения туда, где ожидается среднее значение. Шкала задает размер ожидаемого стандартного отклонения.
По-умолчанию loc=0.0, scale=1.0, что дает стандартное нормальное распределение.
Если при z-нормализации мы отнимаем среднее и делим на стандартное отклонение, то при генерации распределения с заданными параметрами мы прибавляем среднее (задаем loc) и умножаем на стандартное отклонение (задаем scale).
Попробуем сгенерить выборку с заданными параметрами и посчитаем ее среднее и стандартное отклонение.
x = normal(loc=50, scale=10, size=30)
hist(x, density=True, label='выборка')
M=mean(x); S=std(x);
xx = arange(M-4*S, M+4*S, 0.01) #подробные значения абсцисс для гладкой кривой
yy = stats.norm.pdf(xx, M,S)
plot(xx, yy, 'r-', label='модель'); legend(); xlabel('у.е.');
title(f'среднее = {M:.3f}, стандартное отклонение = {S:.3f}');
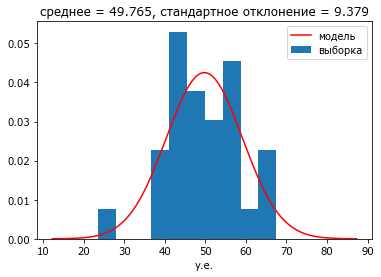
На полученном рисунке можно проиллюстрировать основную догму классической статистики.
Генеральная совокупность (population) - гипотетическая и потенциально бесконечная группа объектов. В данном случае мы получаем её искусственно, и поэтому знаем её истинные параметры - это те параметры, с которыми мы запускаем генератор случайных чисел - среднее 50 и стандартное отклонение 10.
Из этого потенциально бесконечного множества мы извлекли достаточную с точки зрения практической статистики выборку (sample) из 30 значений. В реальной практике эти значения - всё что у нас есть для проведения статистического анализа по результатам экспериментов. Мы считаем выборочные параметры и используем их как приблизительную оценку параметров генеральной совокупности. В данном случае среднее - 49.765, а стандартное отклонение - 9.38.
Классическая статистика разработала математический аппарат для того, чтобы по выборочным оценкам судить о недоступных для непосредственного измерения параметрах генеральной совокупности. Эти суждения носят вероятностный характер. В каждом случае используется свой критерий. Например, можно предсказать, что с вероятностью 95% реальное среднее значение генеральной совокупности (математики говорят математическое ожидание) будет находиться близко к выборочному среднему в интервале от 48.05 до 51.48. То есть, если мы будем извлекать такие выборки снова и снова (например, сто раз), то в 95% случаев эмпирическое выборочное среднее попадет в этот интервал. Такой интервал называется доверительный интервал (confidence interval).
Еще раз обратим внимание, что истинные параметры генеральной совокупности недоступны для измерения, и в данном случае мы их знаем только потому, что мы генерировали искусственные данные с заранее известными характеристиками распределения.
Генерация случайных выборок - это особый вид экспериментов с числами - вычислительные эксперименты. С помощью вычислительных экспериментов можно проверять эффективность различных статистических методов при оценке параметров сложных математических моделей.
Также можно сгенерить выборки для других важных статистических распределений.
np.random.standard_t - \(t\) Стьюдента
np.random.chisquare - \(\chi ^2\) (хи-квадрат)
np.random.exponential - экcпоненциальное
np.random.binomial - биномиальное
np.random.poisson - Пуассона
См. Полный список в документации
Функции для генерации входят в модуль random пакета numpy, поэтому полный путь к ним будет, например, таким: np.random.normal(). Однако при использовании команды %pylab они становятся доступны без преамбулы. Чтобы убедиться, что переменные ссылаются на один и тот же объект используют оператор is.
np.random.binomial is binomial
True
Попробуйте сгенерить выборки для всех упомянутых видов распределений. Для некоторых из них необходимо указать параметры (см. справку к этим функциям:
Shift-Tabпосле открывающей скобки). При этом обратите внимание на то, как параметры влияют на форму гистограммы.
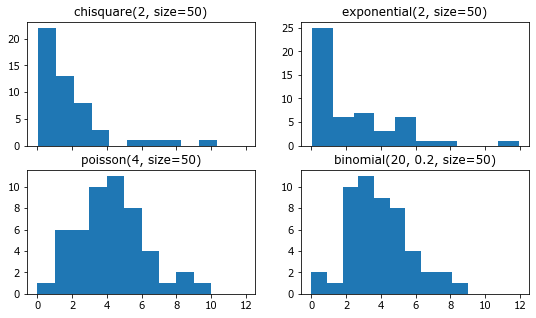

Рис. 4 Гистограммы выборок одного размера, сгенерированных для разных типов распределений.¶
Давайте экспериментально убедимся, что распределение Стьюдента при повышении степеней свободы переходит в нормальное.
Сравним генерацию выборок с моделями, вычисленными по формулам. Функции для работы со статистическими моделями доступны в модуле scipy.stats. Для каждого распределения можно получить моменты, PDF (Probability density function, плотность распределения), CDF (Cumulative distribution function), PPF (Percent point function) и др. производные от них функции.
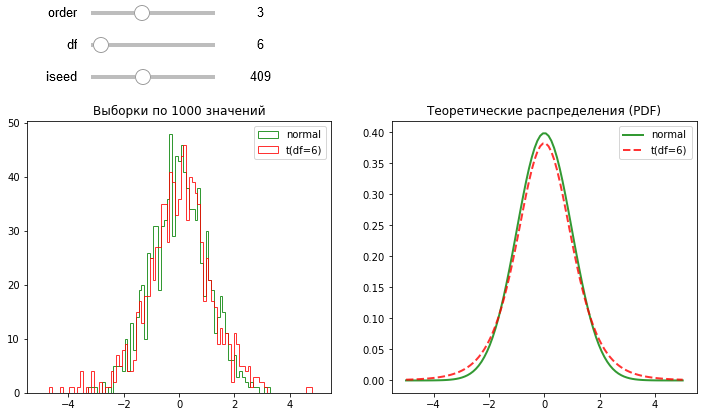
Рис. 5 Сравнение эмпирических и теоретических распределений Стьюдента и нормального¶
При повышении параметра \(df\) степени свободы распределение Стьюдента становится неотличимым от нормального. Параметр степень свободы на 1 меньше количества экземgляров в выборке. \(df=6\) соответствует выборке из 7 объектов. Это считается маленькой выборкой.
Отличие \(t-\)распределения Стьюдента от нормального связано с более толстыми хвостами, то есть вероятность отклонения значений дальше от центра чуть выше, чем у нормального распределения. Поскольку часть вероятности «уходит» в хвосты, то вершина чуть ниже.
При размере выборки 30 и выше различия полностью нивелируются, поэтому считается, что при таких выборках распределения Стьюдента утрачивает своё преимущество. На малых же выборках «толстохвостое» распределение даёт более точные оценки параметров локализации и разброса.
Размер выборки экспериментальных данных, при котором гистограммы эмпирических распределений начинают соответствовать теоретическим, составляет \(10^4...10^5\). При меньших размерах форма эмпирических распределений сильно варьирует и различия между распределениями скрадываются.
Для представления о том, настолько вариативны выборки при одних и тех же характеристиках генераторов, подвигайте бегунок параметра iseed.
Если в выборках из сотни значений основная плотность всегда распределена около нуля, то в выборках из десятка значений иногда попадаются случаи, когда большинство значений одного цвета сильно смещены в одну половину диапазона.
Также, в одних случаях все исходы компактно группируются между -2 и 2, то в других сразу несколько значений могут выйти за границы 3 стандартных отклонений от центра.
Развитие интуиции о принципиальной неустойчивости выборочных оценок полезно для специалистов, которым приходится интерпретировать результаты нативных наблюдений с небольшим количеством данных.
Воспроизводимая генерация случайных чисел¶
Генератор случайных чисел (ГСЧ) работает по специальному алгоритму так, что следующее сгенерированное число невозможно предсказать.
Примечание
В большинстве современного программного обеспечения используется алгоритм, разработанный в 1997 году под названием Вихрь Мерсенна. «Вихрь» — это преобразование, которое обеспечивает равномерное распределение генерируемых псевдослучайных чисел в 623 измерениях. Псевдослучайная последовательность, порождаемая вихрем Мерсенна MT19937, имеет очень большой период, равный числу Мерсенна \(2^{19937} − 1\) (более \(10^{6001}\)), что более чем достаточно для многих практических приложений.
Однако, это чёткий алгоритм, и если запустить его из идентичного состояния, то получится идентичная последовательность чисел. Это очень удобно для исследований и демонстрации конкретных исходов экспериментов с генерацией распределений.
Состояний для запуска ГСЧ может быть очень много. Для выбора конкретного состояния используется функция seed() (англ. семя, сеять).
Вспомните фразу: «игрок, посеянный под 7-м номером». Т.е. это семя, с которым «сеют» случайные числа.
seed(1234567)
hist(binomial( 20, 0.7, size=20));
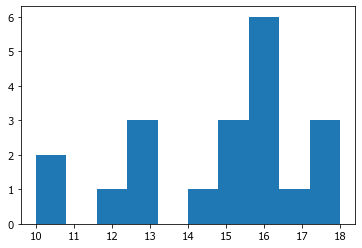
Аргументом функции seed() может быть любое целое число, сколь угодно большое, а также отрицательное.
Отменить действие «фиксированного» в каком-то состоянии ГСЧ можно запуском команды без аргумента или с нулем seed(0).
Попробуйте многократно выполнить код для генерации гистограммы распределения на последнем рисунке, меняя семя на другие числа и на 0.
Для наглядности скопируйте ячейку и вставьте тут же. Если задать одинаковое число для инициализации ГСЧ, то получатся идентичные рисунки.
В командном режиме для получения дубликата ячейки достаточно нажать клавиши CV.
Идентичный рисунок (полученный на идентичной последовательности чисел, сгенерированных ГСЧ в одинаковых состояниях) будет получаться не только на Вашем компьютере, но и на любом другом компьютере во всем мире, где установлена похожая версия программного обеспечения. Эта особенность делает возможным создание расчётных заданий, в которых на каком-то этапе используются случайные числа.
