Выделение событий в сигнале
Выделение событий в сигнале¶
Допустим, вам прислали для сравнения две записи ЭКГ. Специалист, получивший эти записи, работал в MATLAB, где он создал инфраструктуру для манипуляции множеством записей. Две из них в формате struct он сохранил в формате MATLAB и передал Вам.
Функция для загрузки файлов в формате MATLAB есть в пакете scipy.
import scipy.io
import scipy.signal
u=r'd/ecg.mat'
o=scipy.io.loadmat(u)
o.keys()
dict_keys(['__header__', '__version__', '__globals__', 'ecg1', 'ecg2'])
Поля, начинающиеся с двойных подчеркиваний, содержат метаданные файла.
o['__header__']
b'MATLAB 5.0 MAT-file, Platform: PCWIN64, Created on: Wed Nov 27 19:56:09 2013'
Кроме метаданных в файле две переменные: „ecg1“ и „ecg2“.
o['ecg1'].dtype
dtype([('data', 'O'), ('name', 'O'), ('name_col', 'O'), ('type', 'O'), ('units', 'O'), ('freq', 'O'), ('source', 'O'), ('date', 'O'), ('begin_time', 'O'), ('version', 'O'), ('data_quality', 'O'), ('history', 'O')])
По-умолчанию, переменная формата struct - структура, которая загружается в формате записи numpy: 1 структура - 1 запись.
o['ecg1'].shape
(1, 1)
o['ecg1'].dtype.fields
mappingproxy({'data': (dtype('O'), 0),
'name': (dtype('O'), 8),
'name_col': (dtype('O'), 16),
'type': (dtype('O'), 24),
'units': (dtype('O'), 32),
'freq': (dtype('O'), 40),
'source': (dtype('O'), 48),
'date': (dtype('O'), 56),
'begin_time': (dtype('O'), 64),
'version': (dtype('O'), 72),
'data_quality': (dtype('O'), 80),
'history': (dtype('O'), 88)})
Преобразуем структуру в серию pandas.
d = {k:o['ecg1'][0][0][k].squeeze() for k in o['ecg1'].dtype.fields} #.squeeze() чтобы убрать лишние измерения
d = pd.Series(d)
d
data [-6669.0, -6743.0, -6810.0, -6729.0, -6636.0, ...
name Электрокардиограмма
name_col ecg
type 1
units mV
freq 250
source []
date 22-Apr-2010
begin_time 0
version 5.16
data_quality 4
history Created by eegdata2oECG 1
dtype: object
Очевидно, данные находятся в поле data.
y = (d['data'])
plot(y)
y.shape
(78000,)
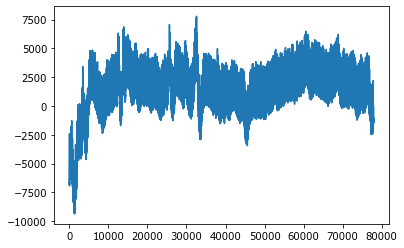
Посмотрим фрагмент подробнее.
plot(d['data'][17000:18000]);
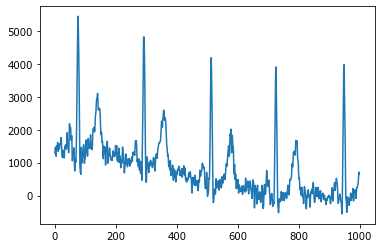
Да это же кардиограмма! Мы знаем, что сердце бьётся примерно один раз в секунду, однако числа по оси Ox не похожи ни на секунды, ни на миллисекунды.
В поле freq мы обнаруживаем частоту сигнала.
Частота в Гц - это сколько отсчетов сигнала помещается в 1 с.
freq = float(d['freq'])
freq
250.0
Для второй записи извлечем данные напрямую, поскольку мы уже изучили структуру данных.
y2 = o['ecg2'][0][0]['data']
y2.shape
(150800, 1)
Наложим два сигнала, задавая попарно координаты x и y через запятую.
x=arange(0, len(y)/freq, 1/freq)
x2=arange(0, len(y2)/freq, 1/freq)
plot(x,y, x2,y2, alpha=.7)
xlabel('time, s'); ylabel('ecg, $\mu V$'); legend(['ecg1','ecg2']);
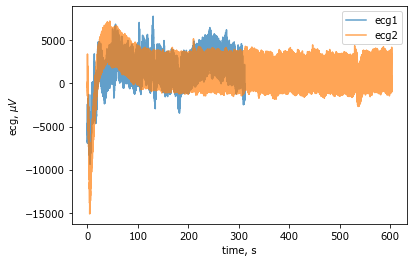
Видно, что первая запись продолжалась около 5 мин, а вторая запись длиннее - около 10 мин. При этом в начале записи сильно отклоняются от нуля.
Чтобы убрать колебания изолинии - профильтруем сигнал фильтром низких частот.
# делаем фильтр с пропусканием выше 2 Гц
b, a = scipy.signal.firwin(int(freq/2), 2/(freq/2), pass_zero=False), 1
# запускаем фильтр без сдвига фазы
yf = scipy.signal.filtfilt(b,a,y)
# смотрим эффект на картинке
plot(x,y, x,yf,'r');
xlabel('time, s'); ylabel('ecg, $\mu V$'); legend(['ecg1','ecg1 filtered']);
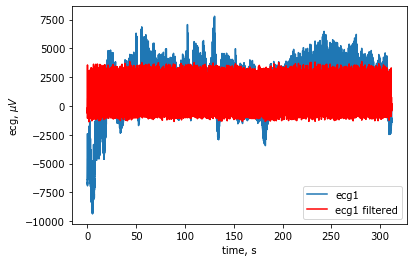
Посмотрим поближе на фрагмент записи, чтобы определить надежный порог для поиска R-зубцов.
Меняйте начальную точку для отображения разных фрагментов.
t0 = 58 # начальная точка просмотра, попробуйте поменять
porog=1200 # порог
i0=int(t0*freq)
ii=slice(i0,i0+int(4*freq))
plot(x[ii],yf[ii],'r');
hlines(porog, x[ii][0], x[ii][-1], 'k','--');

Следующий шаг после подбора порогового значения (показан пунктиром на пред. рисунке) - выделить участки выше порога и найти их пиковые значения.
Конечно же существуют специальные пакеты для подсчета пульса по записи ЭКГ с учетом инверсии сигнала, помех и т.д. Данный алгоритм служит для демонстрации принципов анализа сигналов.
# находим участки сигнала выше порога
#вначале один
i=500
iStart = i + argmax(yf[i:] > porog) # начало зубца - превышение порога
iEnd = iStart + argmin(yf[iStart:] > porog) # конец зубца
ii=slice(iStart,iEnd)
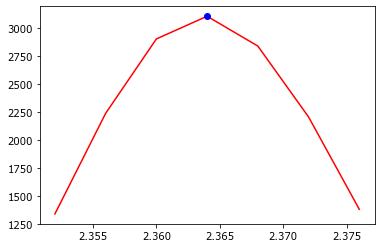
plot(x[ii],yf[ii],'r');
iR= iStart + argmax(yf[ii])
plot(x[iR], yf[iR], 'bo');
# теперь повторим это для всех участков
# введем мертвую зону 400 мс, чтобы не попадать на высокие Т-зубцы
nDead=int(0.4*freq)
rr=[]
i=0
while i< len(yf): # двигаемся вдоль графика
iStart = i + argmax(yf[i:] > porog) # начало зубца - превышение порога
if iStart == i:
break
iEnd = iStart + argmin(yf[iStart:] > porog) # конец зубца
ii=slice(iStart,iEnd)
iR= iStart + argmax(yf[ii])
_r=[x[iR], yf[iR]]
rr.append(_r)
i=iEnd+nDead #прыгаем через "мертвую зону"
rr.__len__()
376
Найдено 376 сокращений на 300-секундной записи.
rr = array(rr)
hist(rr[:,1]); xlabel('Амплитуда пиков, мкВ'); ylabel('Частота');
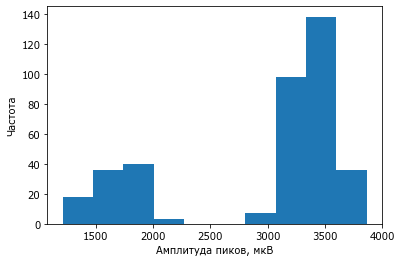
Выделяются два вида зубцов - высокие и низкие (примерно в половину от амплитуды высоких).
Посмотрим как варьируют интервалы между найденными зубцами.
drr=diff(rr[:,0])
hist(drr); xlabel('Интервалы между сердечными сокращениями, с'); ylabel('Частота');
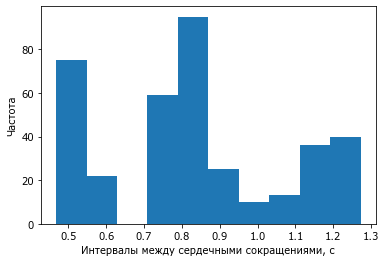
Чаще всего встречались интервалы около 0.8 с (нормальное сердцебиение), также было значительное количество около 0.5 с, и еще одна группа около 1.2 с.
Нарушения ритма могут иметь разные причины. Один из подходов - сопоставить аномальный сердечный цикл с соседними, например, с предыдущим. Для наглядности отложим по горизонтальной оси длительность интервала, а по вертикальной - длительность предыдущего по отношению к нему.
scatter(drr[1:], drr[:-1]);
xlabel('Текущий кардиоцикл'); ylabel('Предыдущий кардиоцикл');

Если сердце бьётся нормально, то и текущий, и предыдущий интервалы равны примерно 0.8 с. Найдите это пересечение. Если человек расслабился, сердечный ритм замедлился, то интервал 0.9 по обеим осям - верхняя правая часть центрального облака. Облако вытянуто наискось, что означает, что частота сокращений изменяется плавно. Теперь найдем экстрасистолы с интервалом 0.5 с. Перед ними всегда был нормальный интервал около 0.8 с (левое облако точек). После экстрасистолы всегда возникала пауза (правое нижнее облако). И осталось последнее верхнее облако - после паузы больше секунды всегда следовало нормальное сокращение.
Мы видим четкие четыре обособленных группы значений! У этого человека серьезные проблемы с сердечной регуляцией. Это пример диагностики без использования статистических методов. Подробности см. Экстрасистолия
