Содержание

Компоненты нелинейного процесса

Компоненты нелинейного процесса

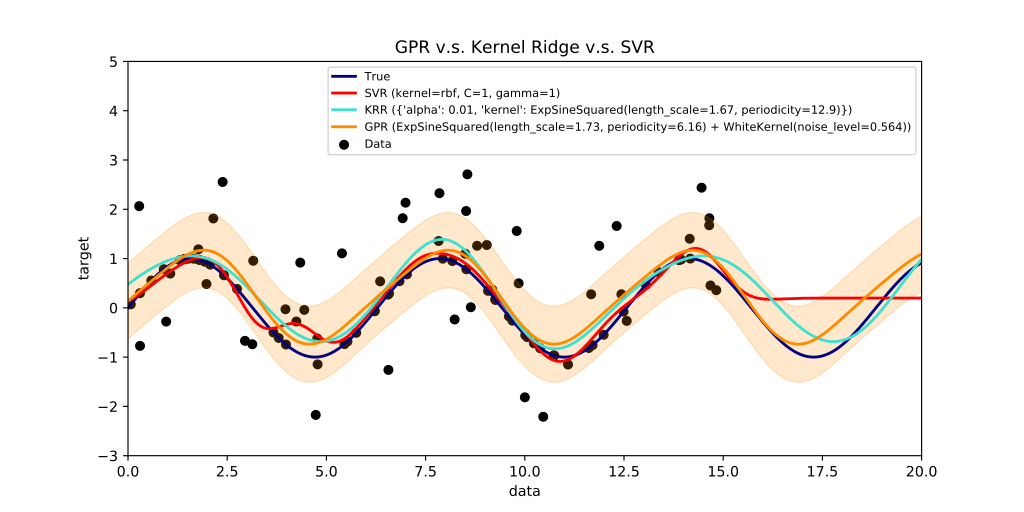
Для процессов, в которых есть периодические составляющие, прогнозные модели на основе простой экстраполяции текущего состояния работают плохо. В правой части рисунка (Рис. 16), где данные (черные точки), представляющие собой синусоиду (темно-синяя линия) с шумом, закончились, видно, что регрессионная модель SVR (красная линия) не может прогнозировать продолжение колебаний, останавливаясь на некотором уровне. Модели KRR и GPR (голубая и оранжевая линии) способны прогнозировать будущие колебания. Модель GPR (Gaussian Process Regression) кроме среднего значения предсказывает дисперсию (область разброса) значений: область наиболее вероятного появления данных с учётом шума показана полупрозрачным оранжевым поясом вокруг оранжевой линии.

Рис. 16 Сравнение различных моделей трендов. GPR - Gaussian Process Regression. ©

Подберем параметры Гауссова процесса для данных в тесте ускорения нажатий. Подставьте ссылку на собственные данные, если вы прошли тест по инструкции.

import pandas as pd

from sklearn.gaussian_process import GaussianProcessRegressor
from sklearn.gaussian_process.kernels import RBF, WhiteKernel, ConstantKernel as Constant, \
        Matern, PairwiseKernel, Exponentiation, RationalQuadratic

u='http://stireac.com/uskor/result.tsv/sherdim%40gmail.com/10.132.32.111__6158019760000190311'
M = pd.read_table(u)
M = M.rename(columns={'v':'code'})
M.info()

<class 'pandas.core.frame.DataFrame'>
RangeIndex: 1000 entries, 0 to 999
Data columns (total 2 columns):
 #   Column  Non-Null Count  Dtype  
---  ------  --------------  -----  
 0   t       1000 non-null   float64
 1   code    1000 non-null   int64  
dtypes: float64(1), int64(1)
memory usage: 15.8 KB

Извлечем из списка маркеров информацию о нажатиях с разбивкой по этапам.

R = []
for itrial in range(6):
    coab = (1000 + itrial)+1
    tab = M.t[M.code==coab].iloc[0]
    tad = M.t[(M.t>tab) & (M.code==13)].iloc[0]
    _R = M[(M.t>=tab)&(M.t<tad)].copy()
    _R['trial']=itrial+1
#     _R['d']=np.nan
    # оставляем только нажатия (коды отжатия < 0)
    _R = _R[(_R.code > 20) & (_R.code < 100)]
    # выравниваем по времени относительно начала этапа
    _R.t -= tab
    _R.dropna(inplace=True)
    _R['iri'] = _R.t.diff()
    
    R.append(_R)
    
R = pd.concat(R)
R.shape

(445, 4)

Этапы отличаются между собой порядком нажатия на кнопки F и J, коды которых маркируют моменты нажатия.

(ord('F'), ord('J'))

(70, 74)

R.groupby(['trial','code']).code.count()

trial  code
1      70      48
2      74      45
3      70      43
       74      43
4      70      48
       74      49
5      70      22
       74      62
6      70      60
       74      25
Name: code, dtype: int64

Создадим справочную таблицу с паттернами этапов.

S = pd.DataFrame([
['00000000', 'одна рука'],
['11111111', 'одна рука'],
['10101010', 'поочередно'],
['01010101', 'поочередно'],
['01110111', 'паттерн'],
['10001000', 'паттерн'],
    ], columns=['pattern','тип'], index=arange(6)+1)
#S

Рисунок с нелинейными трендами

Для построения рисунка мы для каждого этапа выводим исходные данные и накладываем на них в том же цвете модель (среднее и стандартное отклонение).

Данными, динамику которых мы моделируем, являются интервалы между нажатиями, которые рассчитываются в строке.

vv = np.diff(tt)

Обученная модель Гауссова процесса хранится в переменной gpor. Из объекта модели мы извлекаем ряд параметров, которые сводим в таблицу параметров P, которую выводим в конце.

fig, ax = plt.subplots(1, 1, figsize=(12,5))

kernel = (Constant(1**2, (1e-6, 2.)) 
        + 0.05 * Matern(length_scale=20.0, length_scale_bounds=(3, 1e3), nu=1.5)
        + WhiteKernel(noise_level=1e-2, noise_level_bounds=(1e-5, 1e3))
         )
k = 1.

papa = []
coco = cm.tab20(arange(6))
for itrial, co in zip(arange(6)+1, coco):
    _R = R[R.trial==itrial]
        
    if len(_R)<5:
        continue
        
    tt = _R.t.values[1:] - _R.t.values[0]
    
    tt = tt[np.isfinite(tt)]
    vv = np.diff(tt) #_R.iri.values[1:]
    bb = vv < 1.6
    tt, vv = tt[np.r_[True, bb]], vv[bb]
    
    X = np.reshape(tt[1:],(-1,1))
    y = np.reshape(vv,(-1,1))
    gpor = GaussianProcessRegressor(kernel, alpha=1e-5, n_restarts_optimizer=0).fit(X, y)

    pa = {'label':S.loc[itrial, 'pattern']}
    pa['R2'] = gpor.score(X,y)
    pa['LML'] = gpor.log_marginal_likelihood_value_
    pa['n'] = len(vv)
    pa['totalvar'] = np.var(vv)
    _th = np.exp(gpor.kernel_.theta)
    pa['const'] = np.sqrt(_th[0])
    pa['a'] = np.sqrt(_th[1])
    pa['period'] = _th[2]
    pa['noise'] = _th[3]
    papa.append(pa)

    
    plot(tt[1:],vv,'.', color=co, alpha=.5, label='_nolegend_')

    xx = tt
    y_mean, y_std = gpor.predict(xx[:,np.newaxis], return_std=True)
    y_mean = y_mean.flatten()
    plt.plot(xx, y_mean, color=co, lw=4, alpha=.8, zorder=9, label=pa['label'])
    plt.fill_between(xx, y_mean - k * y_std, y_mean + k * y_std,
                     alpha=0.1, color=co)

plt.xlabel('Время, с');
plt.ylabel('Интервал между нажатиями, с');
# plt.ylim(0,1.2)
legend(frameon=False);
        
P = pd.DataFrame(papa)
P = P.set_index('label')
display(P[['const','a','period','noise', 'LML','R2']])
const a period noise LML R2
label
00000000 0.001222 0.497643 11.969143 0.000298 98.296158 0.993221
11111111 0.483434 0.706720 10.677941 0.000237 86.502677 0.998162
10101010 0.274411 0.887480 18.219857 0.001319 134.393564 0.984961
01010101 0.003352 1.062370 34.062973 0.001981 142.929722 0.978169
01110111 0.003453 0.929588 24.105527 0.000766 138.942631 0.993141
10001000 0.640024 0.646241 13.025212 0.001462 120.531530 0.989695
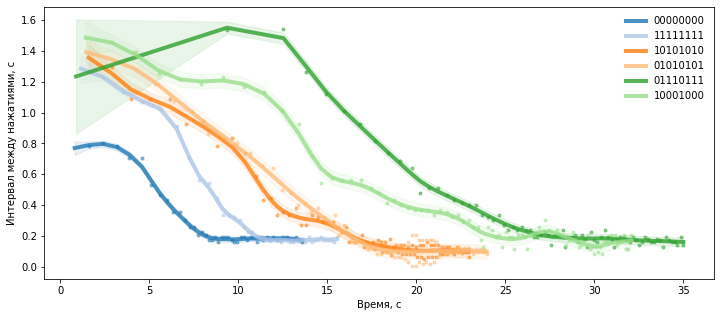
_images/i_gaupro_15_1.png

По параметру period можно сравнить выявленный колебательный компонент в с. Более пологий спуск соответствует более длительному периоду колебаний.

Попробуйте поменять параметры регуляризации при обучении Гауссова процесса. Гиперпараметр alpha, по умолчанию равный 1e-10 (0.0000000001), нужен для предотвращения потенциальных вычислительных проблем во время подгонки модели. Если его увеличить (сделать не таким ничтожным), то будут подобраны более плавные модели, не повторяющие столь подробно динамику процесса. Повышайте параметр alpha на порядок, начиная от 1e-3 до 1e0. Как изменяются параметры найденных моделей? В какой момент модели утрачивают способность описать переходный процесс? Игнорируйте предупреждения о проблемах сходимости модели.

Гиперпараметр - это параметр для управления процессом обучения по подбору других параметров.

Прогноз

Воспользуемся уже рассмотренными ранее способами оценки качества прогноза для одного из этапов.

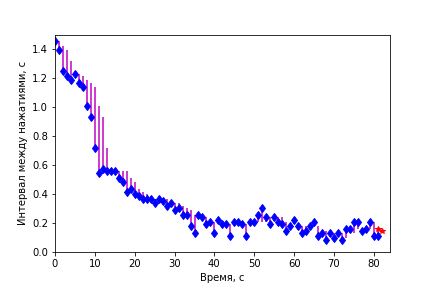
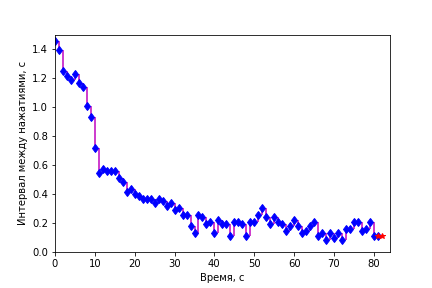
def play_prognoz(k='prognoz', n_future = 1, k0='v', interval=500):

    xx=D.index.values
    tt= xx[:-1]

    fig = figure()
    xlim(0,len(D.index)+1); ylim(0,1.5);

    hh=[]
    hh.append( plot([],[], color='b', lw=0, marker='d')[0] )
    hh.append( plot(xx[0],D[k][0], color='r', marker='*')[0] ) #prognoz
    hh.append( vlines([],[],[], colors='pink') ) #residuals
    xlabel('Время, с');
    ylabel('Интервал между нажатиями, с');
    
    def updatefig(i):
        hh[0].set_data(xx[:i+1], D[k0][:i+1])
        hh[1].set_data(xx[[i,i+n_future]], D[k][[i,i+n_future]])
        res1=vstack([tile(xx[i],(2,)), [D.loc[i,k0],D.loc[i,k]]]).T
        hh[2].set_segments((hh[2].get_segments() + [res1]))
                            
        return hh

    close()
    ani = animation.FuncAnimation(fig, updatefig, tt, interval=interval, blit=True, repeat=False)
    return ani

Переменные vv и y_mean содержат данные и предсказания Гауссова процесса для последнего 6-го этапа. Организуем их в таблицу.

Добавим помимо подогнанной модели Гауссова процесса (не забудьте вернуть гиперпараметр в исходное состояние и получить качественные модели) несколько простых сглаживающих моделей.

D = pd.DataFrame(vv, columns=['v'])#, index=tt[1:])

D['pro_gaupro'] = y_mean[1:]

D['pro_prev']= D.v.shift()
D['pro_median5']=D.v.rolling(5, min_periods=1).median().shift()
D['pro_mean5']=D.v.rolling(5, min_periods=1).mean().shift()
D['pro_ewma']=D.v.ewm(span=5, min_periods=1).mean().shift()

play_prognoz('pro_median5')


play_prognoz('pro_prev')


def quo(k):
    '''чем больше отклонение - тем ниже эффективность'''
    return 1/sqrt(mean((D.v - D[k])**2))

# vidy = [_k for _k in D.columns if _k.startswith('pro_')]
vidy = ['pro_prev', 'pro_mean5', 'pro_median5', 'pro_ewma', 'pro_gaupro']
Q = pd.Series(map(quo, vidy), index=vidy)
Q

pro_prev       16.387643
pro_mean5       9.907941
pro_median5     9.497796
pro_ewma       10.681131
pro_gaupro     20.683305
dtype: float64

Прогноз по предыдущему значению имеет преимущество для резких переходных процессов, поскольку обладает минимальной «памятью» о прошлых значениях.

Компоненты процесса можно вычитать из общей динамики, и, таким образом, строить прогнозы с учетом разных сочетаний компонентов: медленных трендов, циклов, шума.

назад

Предсказание будущих реакций на основе предшествующих

вперёд

Структурные модели