Содержание

Переходные процессы

Переходные процессы

Ряды значений при смене состояния в системе часто имеют вид ступеньки. Ситуация смены состояния присутствует в тесте «Ускорение нажатий».

Загрузим маркеры и извлечем данные для первого этапа одного из тестов.

#u='http://uskor.stireac.com/result.tsv/sherdim%40gmail.com/10.132.32.111__6158019760000190311'
u = 'm__10.132.32.111__6158019760000190311.tsv'
M = pd.read_table(u)

coab, coad = 1001, 13
tab = M.t[M.v==coab].iloc[0]
tad = M.t[(M.t>tab) & (M.v==coad)].iloc[0]
R = M[(M.t>=tab)&(M.t<tad)].copy()
# оставим только клавиши - код < 100
R = R[(R.v<100) & (R.v>50)]
R['iri'] = R.t.diff()
R.plot('t','iri', kind='scatter');
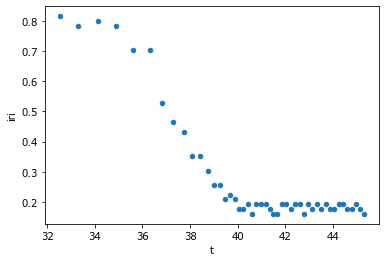
_images/i_perehod_3_0.png

Задача - найти момент перехода от «состояния 0.8» в «состояние 0.2».

Первый способ - наивный: задать порог как середину между «большими» и «маленькими» значениями.

vbig = R.iri.max()  #0.8
vsmall = R.iri.min()  #0.2
porog = vsmall + (vbig - vsmall)/2  #0.5

i = argmax(R.iri < porog)
i

8

R.plot('t','iri', kind='scatter');
axhline(porog, ls='--', color='gray', label='порог')
plot(R.iloc[i].t, R.iloc[i].iri, 'o', markersize=10, mew=2, mec='red', mfc=(0,0,0,0), label='ниже порога')
title('Ускорение на {:.1f} сек'.format(R.iloc[i].t))
legend();
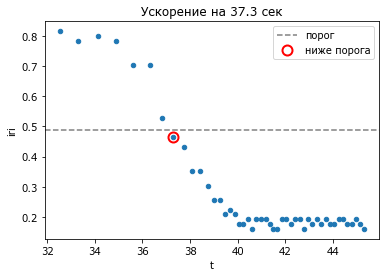
_images/i_perehod_7_0.png

А если значения сильно «прыгают» вверх-вниз?

Можно применить сглаживание сигнала, например, с помощью скользящего среднего.

Логистическая кривая

Переход между двумя состояниями смоделируем плавной кривой, которая сначала 1, а потом 0. В точке, где кривая будет проходить через 0.5, будет момент перехода.

Так как мы хотим плавные переходы, то основываемся на экспоненте. Экспонента известна своим стремительным ростом, а нам надо за пределы 1 не выходить. Чтобы при увеличении экспоненты мы приближались к нулю, перенесем экспоненту в знаменатель \(y = \frac{1}{e^t}\). Там, где время равно 0, экспонента равна 1. Зная это, мы в этом месте зафиксируем функцию на уровне 0.5 или \(\frac{1}{2}\). Для этого в знаменатель прибавим 1!

\[y = \frac{1}{1+e^t}\]
t = arange(-5,5,.01)
y = 1/(1 + exp(t))
y_ = 1/(1 + exp(-t))
plot(t, y, 'r-', label='logistic');
plot(t, y_, 'm-', label='retro logistic');
axhline(0.5, ls='--', color='aqua')
grid(True)
legend();
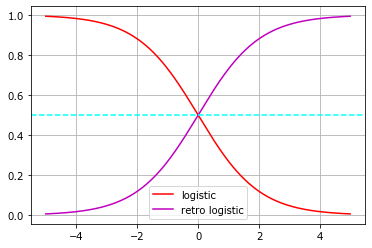
_images/i_perehod_11_0.png

Если пустить время вспять - то есть использовать экспоненциальный спад вместо экспоненциального роста, то получим «отражение» кривой относительно нулевого момента.

Чтобы кривая «двигалась» вдоль оси абсцисс, мы должны добавить в уравнение изменяемый параметр - сдвиг относительно нулевого момента \(t_0\), который мы и хотим найти.

\[y = \frac{1}{1+e^{(t - t_0)}}\]

Логистическое уравнение впервые ввел в обиход бельгийский математик Ферхюльст (Pierre François Verhulst) в 1845 году, который занимался моделированием численности населения. Пьер Франсуа писал по-французски, поэтому произносил название функции как «фонксьОн ложистИк».

Для решения уравнения надо выразить \(t_0\) через \(y\), который нам известен, ведь это и есть наши данные.

\[e^{(t - t_0)} = \frac{1}{y} - 1\]
\[(t - t_0) = log\big(\frac{1}{y} - 1\big)\]
\[t_0 = t - log\big(\frac{1}{y} - 1\big)\]

Второй способ - прокрастинация данных из логистической модели в линейную.

Растянем значения между 0 и 1.

vbig = R.iri.max()  #0.8
vsmall = R.iri.min()  #0.2

t = R.t.values
y = (R.iri.values - vsmall) / (vbig - vsmall)

plot(t, y, '.');
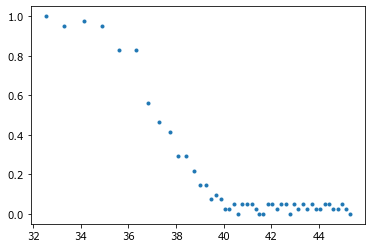
_images/i_perehod_16_0.png

Так как аргументом логарифмической функции должно быть положительное число, то загоним значения в коридор между 0.01 и 1 и преобразуем в линейную зависимость.

y = np.clip(y, 0.01, 0.99)
ylin = log(1/y - 1)
plot(t, ylin, '.');
axhline(0, lw=1, color='gray');
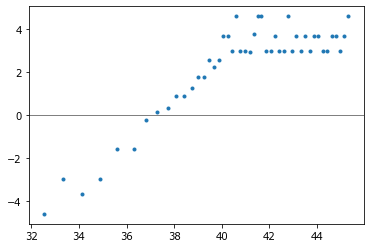
_images/i_perehod_18_0.png

Точечки выстроились в линию, и мы можем найти точку пересечения с осью абсцисс. Числа после 40 с не очень вписываются в зависимость, их мы брать не будем.

bb = (t < 40.5) & isfinite(ylin)
t = t[bb]
ylin = ylin[bb]

Решением линейного уравнения будут такие коэффициенты \(a\) и \(b\), при которых \( \hat{y} = ax + b \) будет максимально близко к \(y\), т.е. остатки \((\hat{y} - y)\) будут минимальными.

Вариант 1. Ручное решение перемножением матриц.

\[\hat{y} = x \cdot a + 1 \cdot b = [x, 1] \cdot [a, b] = X \cdot ab \]
\[ ab \sim y X^{-1}\]
X = vstack([t, ones(shape(t))]).T
X

array([[32.531,  1.   ],
       [33.315,  1.   ],
       [34.115,  1.   ],
       [34.899,  1.   ],
       [35.603,  1.   ],
       [36.307,  1.   ],
       [36.835,  1.   ],
       [37.299,  1.   ],
       [37.731,  1.   ],
       [38.083,  1.   ],
       [38.435,  1.   ],
       [38.739,  1.   ],
       [38.995,  1.   ],
       [39.251,  1.   ],
       [39.459,  1.   ],
       [39.683,  1.   ],
       [39.891,  1.   ],
       [40.067,  1.   ],
       [40.243,  1.   ],
       [40.435,  1.   ]])

ab = ylin.dot(pinv(X).T)
ab

array([  1.01657639, -37.8654124 ])

Вариант 2. Полином 1-й степени.

poly = polyfit(t, ylin, 1)
poly  # Polynomial coefficients

array([  1.01657639, -37.8654124 ])

Вариант 3. Линейная регрессия

res = stats.linregress(t, ylin)
res

LinregressResult(slope=1.0165763888921415, intercept=-37.86541239882312, rvalue=0.9841356925993817, pvalue=5.707543579625563e-15, stderr=0.04319614854900934)

Вариант 4. OLS (ordinary least squares) model

import statsmodels.api as sm
mo = sm.OLS(ylin, sm.add_constant(t)).fit()
mo.summary()
OLS Regression Results
Dep. Variable: y R-squared: 0.969
Model: OLS Adj. R-squared: 0.967
Method: Least Squares F-statistic: 553.8
Date: Wed, 02 Jun 2021 Prob (F-statistic): 5.71e-15
Time: 07:38:19 Log-Likelihood: -11.571
No. Observations: 20 AIC: 27.14
Df Residuals: 18 BIC: 29.13
Df Model: 1
Covariance Type: nonrobust
coef std err t P>|t| [0.025 0.975]
const -37.8654 1.627 -23.271 0.000 -41.284 -34.447
x1 1.0166 0.043 23.534 0.000 0.926 1.107
Omnibus: 3.275 Durbin-Watson: 1.994
Prob(Omnibus): 0.194 Jarque-Bera (JB): 2.086
Skew: 0.791 Prob(JB): 0.352
Kurtosis: 3.054 Cond. No. 603.


Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
mo.params

array([-37.8654124 ,   1.01657639])

Сравните названия, которыми в разных вариантах обозначаются полученные значения.

Обратите внимание, что в двух последних вариантах мы получаем оценку точности полученных значений (stderr).

Наше решение там, где прямая проходит через ось абсцисс. Решаем уравнение.

\[ ax + b = 0 \]
\[ x = - b/a \]
a, b  = ab

t0 = -b/a
t0

37.24797547195505

Так как мы получили оценки точности, то можем посчитать минимальное и максимальное возможные решения с учетом погрешности.

b, a = mo.params
berr, aerr = mo.bse
berr, aerr

(1.6271761689595965, 0.043196148549009196)

t0 = -b/a
t0min = -(b-berr)/(a-aerr)
t0max = -(b+berr)/(a+aerr)
t0min, t0max

(40.57262201445649, 34.19435298574704)

Визуально наложим решение поверх данных.

plot(t, ylin, '.', label='данные');
xx = np.linspace(t[0],t[-1],100)
yy = a*xx + b
plot(xx,yy, 'r', label='модель')
y_std = aerr
k = 2
fill_between(xx, yy - k*y_std, yy + k*y_std, alpha=0.1, color='r')

axvspan(t0min, t0max, color='k', alpha=0.1)
axvline(t0, color='k', alpha=0.8, label='решение')

legend();
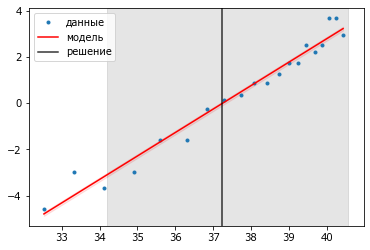
_images/i_perehod_40_0.png

А теперь изобразим модель после преобразования в исходную логистическую зависимость.

Не забываем выполнить депрокрастинацию.

\[y' = (y - v_{small}) / (v_{big} - v_{small})\]
\[y = y' (v_{big} - v_{small}) + v_{small}\]
plot(R.t, R.iri, '.', label='данные');
xx = np.linspace(32,45,100)

# для оригинальной модели нам не нужны a и b - только один параметр t0 !
yyori = 1/(1+exp(xx - t0))
yyori = yyori*(vbig - vsmall) + vsmall
plot(xx, yyori, 'r', label='модель')

yyorimax = 1/(1+exp(xx - t0max)) *(vbig - vsmall) + vsmall
yyorimin = 1/(1+exp(xx - t0min)) *(vbig - vsmall) + vsmall
fill_between(xx, yyorimin, yyorimax, alpha=0.1, color='r')

axvline(t0, ls='--', color='k', label='перелом')
xlabel('Время, с')
ylabel('Интервал, с')
legend();
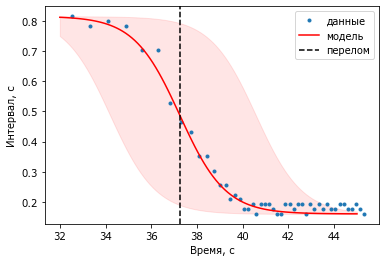
_images/i_perehod_42_0.png

Третий способ - подбор параметров модели.

В полной логистической модели, предполагающей два устойчивых состояния, можно задать четыре параметра.

\[y(x) = { u-d \over 1+e^{-k(x-x_0)} } + d\]

Сделав такую функцию, подборем ее параметры с помощью метода оптимзации curve_fit (подгонка кривой).

def func(x, u, d, x0, k):
    '''Логистическа функция с 4 параметрами
    
    x - данные для преобразования
    u - "верхняя полка"
    d - "нижняя полка"
    x0 - время "прыжка"
    k - крутизна "прыжка"
    
    https://en.wikipedia.org/wiki/Logistic_function'''
    return ((u-d) / (1+( np.exp(-k*(x-x0))))) + d

# данные для подбора
x, y = R.loc[R.iri.notnull(), ['t','iri']].values.T
# x = x - x[0]

popt, pcov = optimize.curve_fit(func, x, y, method='dogbox',
                 p0=[ max(y), min(y), x[-1], .1],
                 bounds=([0, min(y), min(x), -1e8],
                         [max(y), max(y), max(x),  1e8]),
                 #maxfev=5000  
                )
popt

array([ 0.81195291,  0.17677216, 37.27717736, -1.11004778])

Мы получили четыре искомых параметра. Теперь визуализируем результаты. Для генерации модельных значений будем использовать ту же функцию, но для значений х, плавно изменяющихся от минимума к максимуму.

co = 'b'
label = 'модель 1'

#def plot_model(x,y, popt, co, label):
#    '''Функция для рисования данных и модели одним цветом'''
plot(x, y, marker='o', lw=0, color=co, alpha=.8, zorder=3)

xx = linspace(x.min(), x.max(), 200)
yy = func(xx, *popt)
plot(xx,yy, color=co, ls='-', label=label, zorder=10);

axhline(popt[0], color='r', ls='--', alpha=.6, label='верхняя полка')
axhline(popt[1], color='m', ls='--', alpha=.6, label='нижняя полка')
axvline(popt[2], color='k', ls='--', alpha=.8, label='перелом')

axhline(0, color='k', ls='-', lw=1, alpha=.6)

ylabel('Интервал, с')
xlabel('Время, с');
legend();
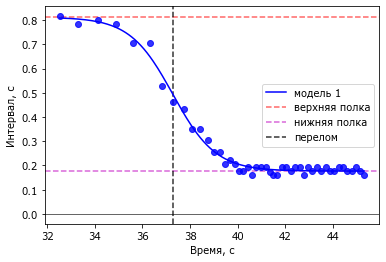
_images/i_perehod_47_0.png

Для наложения нескольких рисунков один поверх другого удобно иметь в распоряжении функцию, параметрами которой будут данные и параметры отображения - цвет и подпись. При повторном вызове функции можно получить сложный разноцветный рисунок.

Чтобы получить из предыдущего фрагмента кода функцию:

  1. Раскомментируйте строку определения функции и ее описания

  2. Сдвиньте весь нижележащий код вправо на 4 пробела.

#plot_model(x,y, popt, co, label)
#plot_model(x+2,y+0.1, popt+[.1,.1,2,0], 'orange', 'другой процесс')
#plot_model(x+3,y-0.1, popt+[-.1,-.1,3,0], 'green', 'совсем другой процесс')

Нормализация в фиксированном диапазоне

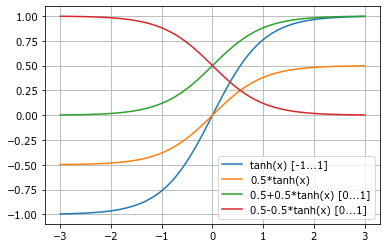
На рисунке Рис. 15 Вы можете увидеть две наиболее часто используемых функции для перевода неограниченных значений в ограниченный диапазон от 0 до 1 и от -1 до 1 .

Функции выходят на плато с разной скоростью: сигмоид (обратная логистическая функция) после 3, а гиперболический тангенс - к 2. Входящий \(x\) можно умножить на коэффициент, чтобы добиться разной степени крутизны подъема функции.

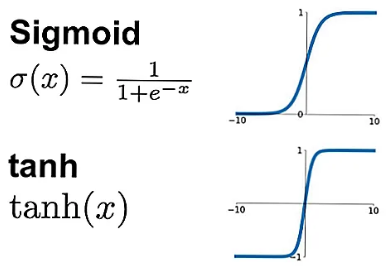
Рис. 15 Функции для нормализации данных в фиксированном диапазоне

Функция гиперболического тангенса полезна для понимания свойств комбинаций экспоненциальных функций. Здесь используются растущие и убывающие экспоненты.

\[tanh\left(x\right) = \frac{e^{x} - e^{-x}}{e^{x} + e^{-x}}\]
x = linspace(-3,3, 100)
y = exp(x) + exp(-x)
plot(x,y, label='сумма');
y = exp(x) - exp(-x)
plot(x,y, ls='--', label='разность');
grid(True);
legend();
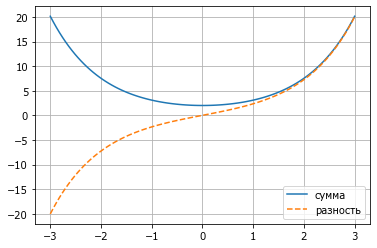
_images/i_perehod_53_0.png

График сумм получается сложением стандартной экспоненциальной функции с обратной ей относительно вертикальной оси. Поскольку экспонента при аргументе меньше 0 убывает, становясь всё меньше единицы, то этот тонкий хвостик не мешает росту обратной функции (с противоположным знаком аргумента) в ту же сторону. Поскольку функции симметричны - образуется «подкова». График разности состоит из дважды зеркально отраженных половинок. Оба графика растут в области положительных значений, и поэтому их отношение всё больше стремится к единице. В области отрицательных значений графики расходятся в противоположные стороны. Поэтому, если мы поделим отрицательные значения для разности на примерно такие же значения для суммы, то получим числа, близкие к -1. В нулевой точке разность разнонаправленных экспонент равна 0, а сумма - 2. \(0/2 = 0\). Поэтому функция гиперболического тангенса проходит через нулевую точку.

y = tanh(x)
plot(x,y, label='tanh(x) [-1...1]');
plot(x, y*0.5, label='0.5*tanh(x)');
plot(x, (1 + y)*0.5, label='0.5+0.5*tanh(x) [0...1]');
plot(x, (1 - y)*0.5, label='0.5-0.5*tanh(x) [0...1]');
grid(True); legend();
_images/i_perehod_55_0.png

назад

🗎 Спектральный анализ

вперёд

Предсказание будущих реакций на основе предшествующих