Увеличение размерности
Увеличение размерности¶
При решении многомерных задач используют подход, разработанный для 1-2 размерностей.
Идея остается прежней, однако вычислительная сложность растет по экспоненте.
Для понимания важным является геометрическая наглядная визуализация зависимостей или алгоритма. Поскольку воспринимать графические визуализации более 3-х измерений сложно, то обычно ограничиваются демонстрацией перехода от 1 к 2 измерениям, а далее по аналогии.
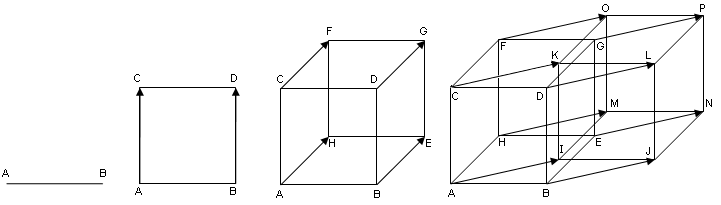
Рис. 20 Увеличение размерности путем экспансии в новом измерении.¶
Часто многомерный вариант понятия получает у математиков особое название. Для практического использования знать их не обязательно, главное понимать смысл базового одномерного понятия.
1-мерный случай |
многомерный случай |
|---|---|
Градиент |
Гессиан - определитель матрицы градиентов |
Биномиальное распределение |
Мультиномиальное распределение |
Бета-распределение |
Распределение Дирихле |
Вариация |
Ковариационная матрица |
Критерий Уилкоксона-Манна-Уитни |
Критерий Краскела-Уоллиса |
В некоторых случаях типичные операторы - + - / * ** становятся двусмысленными при повышении размерности.
Например, среднее может быть для всех чисел в массиве, или для каждой колонки, или для каждой строчки. В этих случаях указываются дополнительные аргументы функции, обычно: axis=0 - по колонкам, axis=1 - по строчкам, и т.д. для более высоких размерностей.
Следует помнить, что все операторы в синтаксисе лишь удобный заменитель соответствующей функции, поэтому если нужно уточнить действие функции - можно пользоваться полным вариантом.
Если нет специального математического оператора, то можно вызвать функцию.
Например, возведение в степень 0.5 имеет специальную функцию sqrt.
sqrt(4) # специальная функция
2.0
4 ** 0.5 # специальный оператор
2.0
pow(4, 0.5) # базовая функция с аргументами
2.0
