Сезонные колебания
Содержание
Сезонные колебания¶
Если есть регулярный вброс энергии или вещества в систему, то из-за экспоненциального спада возникает чередование периодов подъема и спуска. Биологическое значение обычно имеет одна из этих фаз.
В северном полушарии, по сути, два сезона:
лето - активный плодотворный период в природе
зима - период покоя
Остальные - всего лишь переходы, однако именно в переходные периоды идет активная учеба - осенний и весенний семестры. Учеба в общественных и биологических системах - переход от незнания к знанию.
Название активного периода становится единицей счета циклов для измерения интервалов:
активность летом - 5 лет
активность днем - 5 дней
На странице, откуда взят источник данных об истории измерений температуры на метеостанции Ростова-на-Дону, предложены классические графики с динамикой колебаний вдоль одной оси времени.
Так как в дате содержится и год и месяц - мы можем визуализировать временной ряд в двух временных осях без вычисления каких-либо моделей.
Поскольку информация о колонках указана в комментариях, то мы при импорте данных в таблицу указываем параметры
без заголовков (
header=None,)свой перечень кратких имен (
names=[...])
# u='http://berkeleyearth.lbl.gov/auto/Stations/TAVG/Text/169045-TAVG-Data.txt'
u='d/169045-TAVG-Data.txt'
D = pd.read_csv(u, delim_whitespace=' ', comment='%', header=None,
names='year month v0 dv0 q br v dv reg dreg'.split())
D.tail()
| year | month | v0 | dv0 | q | br | v | dv | reg | dreg | |
|---|---|---|---|---|---|---|---|---|---|---|
| 1536 | 2013 | 7 | 24.486 | 1.279 | 0.0 | 0.0 | 24.417 | 1.210 | 23.569 | 0.536 |
| 1537 | 2013 | 8 | 24.419 | 1.928 | 0.0 | 0.0 | 24.408 | 1.916 | 24.037 | 1.720 |
| 1538 | 2013 | 9 | 14.553 | -2.249 | 0.0 | 0.0 | 14.567 | -2.235 | 14.302 | -2.325 |
| 1539 | 2013 | 10 | 8.736 | -0.628 | 0.0 | 0.0 | 8.686 | -0.678 | 8.523 | -0.667 |
| 1540 | 2013 | 11 | 9.600 | 6.366 | 1.0 | 0.0 | NaN | NaN | NaN | NaN |
Как мы видим, данные обрываются на дате 2013-11. В 19-м веке сбор данных также был нерегулярным. Поэтому для целей визуализации отберем колонку «Выверенные температурные данные» за 100 лет.
X = D.loc[D.year>1912, ['year','month','v']]
X.head()
| year | month | v | |
|---|---|---|---|
| 330 | 1913 | 1 | -4.859 |
| 331 | 1913 | 2 | -6.552 |
| 332 | 1913 | 3 | 3.278 |
| 333 | 1913 | 4 | 12.135 |
| 334 | 1913 | 5 | 13.987 |
Готовим названия месяцев (для красоты).
# так можно получить готовый список 3-буквенных названий месяцев на английском
# momo = pd.tseries.frequencies.MONTHS
# momo = list(map(str.capitalize, momo))
# а так мы получим локализованные названия
import locale
locale.setlocale(locale.LC_TIME, '')
momo=[datetime.datetime(2016,i,1).strftime('%b') for i in arange(1,13)]
print(' '.join(momo))
янв фев мар апр май июн июл авг сен окт ноя дек
Группируя по году и месяцу, мы создаем двойной индекс, который методом unstack() разделяем на индекс строк и индекс колонок, получая таким образом широкую таблицу.
W = X[["year", "month", "v"]].groupby(by=["year", "month"]).max().unstack()
W.columns=momo
W.head()
| янв | фев | мар | апр | май | июн | июл | авг | сен | окт | ноя | дек | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| year | ||||||||||||
| 1913 | -4.859 | -6.552 | 3.278 | 12.135 | 13.987 | 17.212 | 21.268 | 23.346 | 16.663 | 7.469 | 4.932 | 1.66 |
| 1914 | -2.559 | 0.648 | 6.878 | 9.135 | 16.487 | 19.612 | 23.368 | 20.246 | 14.563 | 8.669 | -2.168 | -3.44 |
| 1915 | 3.141 | -2.852 | 1.978 | 10.835 | 13.987 | 19.412 | 23.568 | 19.246 | 14.063 | 7.469 | 4.332 | -0.34 |
| 1916 | -3.059 | -2.352 | 1.878 | 9.935 | 15.387 | 19.012 | 22.168 | 19.946 | 13.363 | 9.469 | 3.032 | -2.54 |
| 1917 | -4.459 | -8.952 | -0.522 | 11.935 | 13.087 | 20.412 | 21.468 | 21.546 | 15.963 | 10.369 | 7.332 | -0.84 |
figure(figsize=(12, 8))
sns.heatmap(W, yticklabels=8, cmap="coolwarm")
xlabel('месяц'); ylabel('год'); title('Среднемесячная температура');
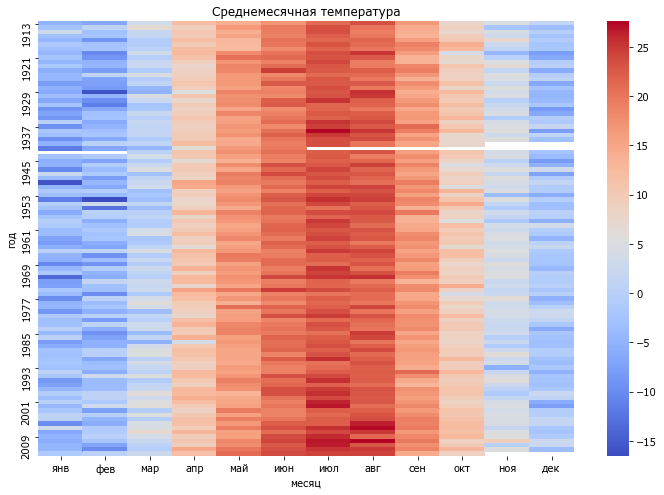
Обратите внимание:
параметр
yticklabelsзадает интервал между отметками по оси, чтобы метки не наезжали друг на друга;дивергентная цветовая карта позволяет сосредоточиться на особо жарких и холодных месяцах;
зимой 1941-го и во время оккупации данные не собирались.
Если у нас стоит задача заполнить недостающие данные или спрогнозировать колебания в будущем, то в условиях стабильных предсказуемых циклов, какими являются сезонными, хороший результат дают средние значения для той же фазы цикла.
В данном наборе данных для прогнозирования температуры в августе в будущем году или заполнения пропуска в 1941 году можно взять среднюю температуру в августе.
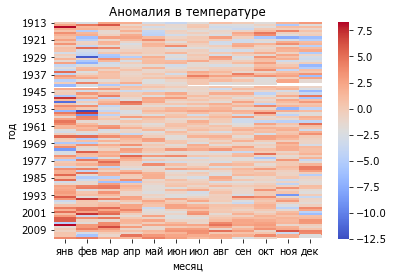
Оценка аномалий¶
В наборе данных есть колонка, показывающая насколько текущее значение отклоняется от ожидаемого, т.е. показывает аномальность температуры в этом месяце.
W_anomal = D.loc[D.year>1912,["year", "month", "dv"]].groupby(by=["year", "month"]).max().unstack() #делаем широкую таблицу
W_anomal.columns=momo
sns.heatmap(W_anomal, yticklabels=8, cmap="coolwarm")
xlabel('месяц'); ylabel('год'); title('Аномалия в температуре');
Сравним аномальность из таблицы с отклонением значений от среднего.
W_dev = W - W.mean()
sns.heatmap(W_dev, yticklabels=8, cmap="coolwarm")
xlabel('месяц'); ylabel('год'); title('Отклонение от среднего');
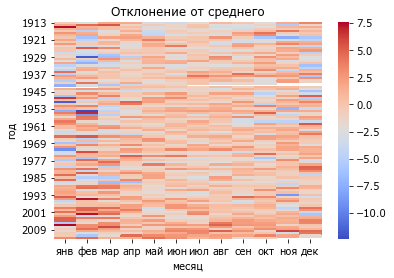
По идентичности рисунков становится понятно, что «аномальность» именно так и рассчитали. Небольшие расхождения в нашем примере связаны с тем, что мы взяли среднее не за всю историю наблюдений, а за 100 лет.
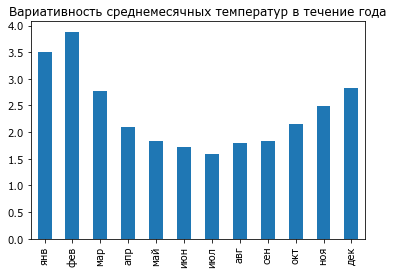
Обратите внимание, что в зимние месяцы температура нестабильна из года в год.
W.std().plot(kind='bar', title='Вариативность среднемесячных температур в течение года');