Содержание

Операции с матрицами

Операции с матрицами

Загрузим координаты изображения из текстового файла, в котором записаны две колонки чисел.

Откуда взялись числа и почему файл называется los см. в задаче Task_dataset_los.

los=loadtxt('d/los.csv', skiprows=1) # параметр skiprows для пропуска заголовков

plot(los,'.'); legend(('1st','2nd')); ylabel('значения'); xlabel('порядковый номер');
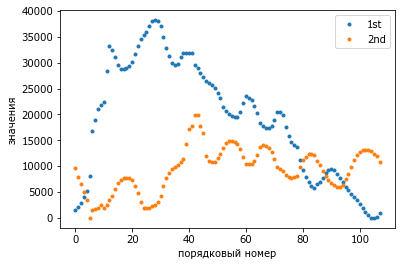
_images/i_matrix_3_0.png

Две колонки чисел - это координаты, поэтому отобразим расположение отдельных значений на пересечении этих координат.

Определим d как копию уже заданной переменой с загруженными данными. Мы хотим обращаться к этим же данным, но использовать короткое имя для переменной, потому что будем многократно писать его в выражениях. Фактически новых данных при этом не создается - создается еще одна ссылка с новым именем на тот же адрес в памяти.

d = los

x=d[:,0];
y=d[:,1];
plot(x,y,'.-'); xlabel('x'); ylabel('y');
_images/i_matrix_5_0.png

Допустим, что исходные значения в мм. Чтобы перевести в м, разделим на 1000, или что то же самое - умножим на 0.001 . Ясно, что при переводе мм в м - картинка не меняется. Меняется лишь шкала по осям координат.

Здесь и далее будем задавать одинаковые размеры по осям координат, чтобы имитировать расположение точек на реальной плоскости.

d = d*[0.001]
x=d[:,0]; y=d[:,1]; plot(x,y,'.'); axis('equal');
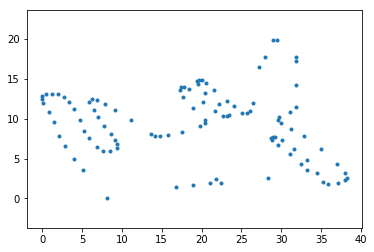
_images/i_matrix_7_0.png

Если мы умножим матрицу на массив (вектор) из двух чисел, то каждая из колонок умножится на свое число. Например, мы можем «сжимать» данные вдоль одной оси, не трогая при этом вторую.

d_ = d*([.25, 1.0])
x=d_[:,0]; y=d_[:,1]; plot(x,y,'.'); axis('square');
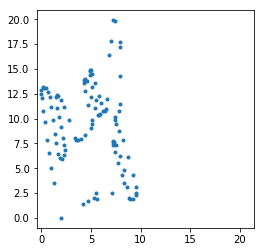
_images/i_matrix_9_0.png

Попробуйте эффект от шкалирования в стационарных координатах.

@interact(k1=(.2,5,.1), k2=(.2,5,.1))
def _scale(k1=1.0, k2=1.0):
    d_ = d*([k1, k2])
    x=d_[:,0]; y=d_[:,1]; 
    plot(x,y,'.-'); axis('square');xlim(0,100);ylim(0,100);
_images/i_matrix_11_0.png

Должно быть ясно, что для получения определенной пропорции достаточно изменить один из коэффициентов.

Согласованное изменение коэффициентов равнозначно изменению единиц шкалы без изменения пропорций. Например, если размеры в см разделить примерно на 4, то получим размеры в дюймах.

Перемножение матриц

Перемножение - главная операция линейной алгебры. В формулах обозначается точкой. Функция называется dot().

\[ A \cdot B = С \]

Результаты умножения каждой колонки из \(A\) на коэффициент из каждой колонки \(B\) суммируются с получением колонки в итоговой матрице \(C\). Получается, что первая строчка \(B\) определяет вклад иксов в итоговые колонки, а вторая строчка - вклад игреков.

Мы можем смешивать вклад обеих колонок в разных пропорциях. Если вклад одной из колонок нам не нужен - мы его обнуляем (перемножаем на 0).

@interact(k1=(.2,5,.1), k2=(.2,5,.1), k3=(-1,1,.1), k4=(-1,1,.1))
def _scale(k1=2.0, k2=3.0, k3=0, k4=0):
    R=array([[k1, k4], [k3, k2]])
    print(R)
    d_ = d.dot(R)
    x=d_[:,0]; y=d_[:,1]; 
    plot(x,y,'.-'); axis('square');xlim(0,100);ylim(0,100);
    

[[ 1.8  0.9]
 [-0.8  2. ]]
_images/i_matrix_14_1.png

Коэффициенты по диагонали (k1, k2) ведут себя точно также, как отдельные множители для каждой из колонок в предыдущих примерах.

Если менять коэффициенты k3 или k4 , то рисунок наклоняется. А если их изменять в противоположных направлениях - рисунок вращается!!!

Чтобы понять, что происходит, вспомним тригонометрию… При вращении (движении точки по окружности) изменяется один параметр - угол \(\alpha\). А координаты точки при этом равны \(sin(\alpha)\) и \(cos(\alpha)\).

Например, чтобы повернуть все точки матрицы на 90 градусов (в радианах \(\frac{\pi}{2}\)), надо от \(x\) отнять \(cos(0)\) и прибавить \(cos(\frac{\pi}{2})\) (из 1 сделать 0), а из \(y\) отнять \(sin(0)\) и прибавить \(sin(\frac{\pi}{2})\) (из 0 сделать 1).

alpha = pi/2
d_ = d.dot([[cos(alpha), sin(alpha)], 
            [-sin(alpha), cos(alpha)]])
x=d_[:,0]; y=d_[:,1]; plot(x,y,'.-'); axis('square');
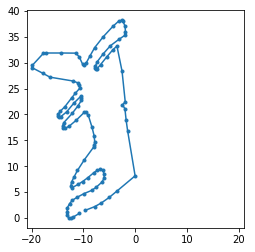
_images/i_matrix_16_0.png 
@interact(alpha=(-180.,360.,5.))
def _scale(alpha=0):
    ro=deg2rad(alpha)
    R=array([[cos(ro), sin(ro)], 
            [-sin(ro), cos(ro)]])
    print(R)
    d_ = d.dot(R)
    x=d_[:,0]; y=d_[:,1]; 
    plot(x,y,'.-'); axis('equal');#xlim(0,100);ylim(0,100);
    title('Вращение на {} градусов'.format(alpha))
    

[[-0.8660254  0.5      ]
 [-0.5       -0.8660254]]
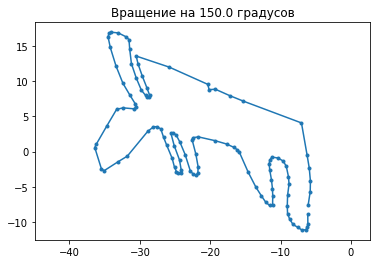
_images/i_matrix_17_1.png

Обратите внимание на коэффициенты при 60, 45, 90, -90, 180, 360 градусах. Бегунок можно двигать стрелочками, если мышкой неудобно.

Вращение на 90 градусов фактически равно замене местами \(x\) и \(y\) и замене знака у \(x\).

Если заменить координаты местами и не заменить знак, то будет «зеркальное» отображение исходной картинки относительно биссектрисы угла.

x=d[:,1]; y=d[:,0]; 
plot(x,y,'.-'); axis('equal');
plot([0,40], [0,40], 'r:');
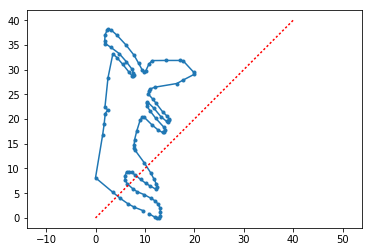
_images/i_matrix_19_0.png

Замена знака у \(x\) и \(y\) соответствует вращению вокруг начала координат на 180 градусов.

x=d[:,0]; y=d[:,1];
plot(-x,-y,'.-'); axis('equal');
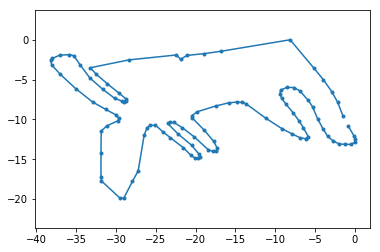
_images/i_matrix_21_0.png

Поправьте элементы матрицы вращения \(R\) так, чтобы изображение лося было правдоподобным, таким, каким его видели жители Урала с вершины горы, когда создавали. Критерий успеха: рога торчат вертикально, спина идет горизонтально.

R=array([[-1, .5], 
         [.25, -1]])
d_ = d.dot(R)
x=d_[:,0]; y=d_[:,1]; plot(x,y,'.-'); axis('equal');
print(R)

[[-1.    0.5 ]
 [ 0.25 -1.  ]]
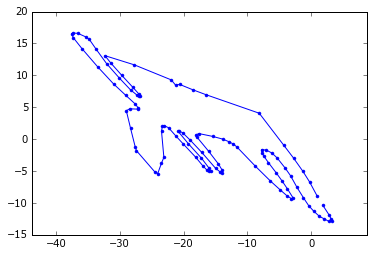
_images/i_matrix_23_1.png

Вывод: сочетание взаимных влияний двух показателей может оказывать эффекты вращения и наклона на паттерн расположения точек в пространстве.

При этом используются простые операции - умножения и сложения. Результат (повернутая матрица) - массив чисел той же размерности с сохраненным взаимным расположением точек. Например, координаты точки из передней ноги в результате любых поворотов и искажений будут находится в промежутке между координатами морды и задней ноги.

назад

Координаты

вперёд

Увеличение размерности