Объединение наборов данных
Содержание
Объединение наборов данных¶
Загрузка данных¶
Посмотрим данные испытуемого, который прошел тест в состоянии усталости и повторно после корректирующей процедуры http://balatte.stireac.com/result/ssdanielyan@mail.ru/ .
udo = 'http://balatte.stireac.com/result.tsv/ssdanielyan%40mail.ru/sta194-1-r401-06.valeo.rsu.ru__6159522610000171030'
uposle = 'http://balatte.stireac.com/result.tsv/ssdanielyan%40mail.ru/sta194-1-r401-06.valeo.rsu.ru__7104549320000171030'
u=uposle
D1=pd.read_table(udo)
D2=pd.read_table(uposle)
D1.shape, D2.shape,
((48, 2), (48, 2))
В ситуации, когда для анализа необходимо объединить два набора данных, необходимо ввести метку для каждого из них, и после этого присоединить один к другому.
D1['isi']=D1.t.diff()
D1['condition'] = 'До'
D2['isi']=D2.t.diff()
D2['condition'] = 'После'
D = pd.concat([D1, D2], ignore_index=True, sort=False)
D.plot('t', 'isi', marker='v', lw=1, figsize=(12,5),
ylabel='МСИ, с',
title='Динамика межстимульного интервала');
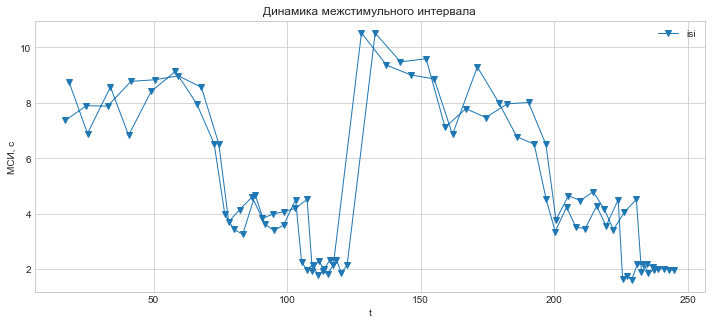
D.condition.value_counts()
До 48
После 48
Name: condition, dtype: int64
Итого в нашей таблице 96 записей.
Добавим информацию об интервале и модальности.
isi0 = array([8,4,2])
momo = ['v','a']
nRep = D1.shape[0]//(len(isi0)*len(momo))
nCond = 2
D['isi'] = kron(isi0, ones((nCond,len(momo),nRep))).reshape((-1,1))
D['mod'] = tile(repeat(momo, nRep*len(isi0)), nCond)
g = D.groupby(['condition','mod','isi'])
g['v'].count()
condition mod isi
До a 2.0 8
4.0 8
8.0 8
v 2.0 7
4.0 7
8.0 8
После a 2.0 8
4.0 8
8.0 8
v 2.0 8
4.0 8
8.0 8
Name: v, dtype: int64
D.isi = pd.Categorical(D.isi.astype(int))
Для каждого условия получили 6 групп по 7-8 значений.
Групповая статистика¶
Вариант 1. numpy.array по параметрам¶
M=g.v.mean()
S=g.v.std()
N=g.v.count()
M=array(M).reshape(nCond, -1)
S=array(S).reshape(nCond, -1)
N=array(N).reshape(nCond, -1)
M
array([[0.287125 , 0.442 , 0.3905 , 0.28285714, 0.352 ,
0.338625 ],
[0.249 , 0.358 , 0.341875 , 0.29 , 0.33 ,
0.292375 ]])
Рассчитанных параметров достаточно для сравнения средних значений между условиями с использованием T-критерия для двух независимых выборок. T-тест также известен как тест Стьюдента.
xx=arange(M.shape[1])
pp=[stats.ttest_ind_from_stats(M[0,i],S[0,i],N[0,i], M[1,i],S[1,i],N[1,i]).pvalue for i in xx]
# pp=[stats.ttest_ind(gg[i],gg[i+3])[1] for i in xx]
pp
[0.36909064312358575,
0.09623013949940952,
0.44410213573195034,
0.8501772924924638,
0.5383907413328164,
0.03312105765225047]
Вариант 2. numpy.array по подвыборкам¶
Отберем множество отдельных групп, и затем сравним их попарно.
gg=[]
for _i,_g in g:
gg.append(_g.v.dropna())
pp=[]
for i in range(M.shape[1]):
pp.append(stats.ttest_ind(gg[i],gg[i+M.shape[1]], nan_policy='omit').pvalue)
pp
[0.36909064312358575,
0.09623013949940952,
0.44410213573195045,
0.8501772924924638,
0.5383907413328164,
0.03312105765225043]
У функции расчета значимости различия средних есть опция equal_var, которой можно отменить допущение о равенстве дисперсии. P-значения будут несущественно различаться.
pp=[stats.ttest_ind(gg[i],gg[i+M.shape[1]], equal_var=False)[1] for i in range(M.shape[1])]
pp
[0.36966271711423226,
0.10449040647410479,
0.44715557863811795,
0.8424489768576212,
0.5406969673300919,
0.03328861661167011]
Мы получили 6 p-values. Всего один результат находится на границе значимости. Значимость различий адекватно оценивается при выборках большего размера.
При повторе одного и того же анализа на соседних выборках нужно использовать поправки на множественные сравнения.
import statsmodels.stats.multitest as multitest
multitest.multipletests(pp, method='fdr_bh')
(array([False, False, False, False, False, False]),
array([0.64883636, 0.31347122, 0.64883636, 0.84244898, 0.64883636,
0.1997317 ]),
0.008512444610847103,
0.008333333333333333)
После поправки p-значения не доходят до уровня значимости 0.05. Первый возвращаемый массив выводит логические значения значимости, второй - p-значения.
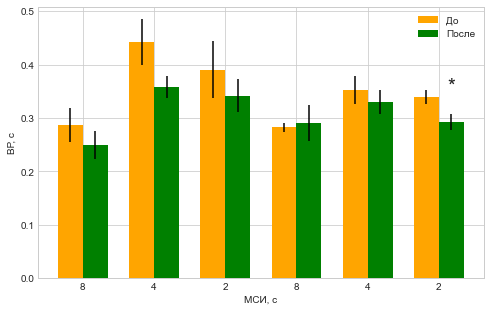
На рисунках значимые различия часто помечают знаком - одной или тремя звездочками.
figsize(8,5)
SEM=S/sqrt(N)
width = 0.35 #ширина столбцов
p1 = bar(xx-width, M[0], width, color='orange', yerr=SEM[0])
p2 = bar(xx, M[1], width, color='green', yerr=SEM[1])
xticks(xx-width/2, tile(isi0,2))
xlabel('МСИ, с')
ylabel('ВР, с')
legend(['До','После'])
for i,p in enumerate(pp):
if p<0.05:
text(xx[i], max(M[:,i])+0.01, '*', size=20, horizontalalignment='center')
Вариант 3. ANOVA с влиянием факторов¶
import statsmodels.api as sm
from statsmodels.stats.anova import anova_lm
В формуле перечисляем колонки с независимыми переменными и их сочетания.
mo = sm.OLS.from_formula('v ~ condition + mod + isi + condition:mod', D).fit()
mo.summary()
| Dep. Variable: | v | R-squared: | 0.253 |
|---|---|---|---|
| Model: | OLS | Adj. R-squared: | 0.210 |
| Method: | Least Squares | F-statistic: | 5.951 |
| Date: | Thu, 03 Jun 2021 | Prob (F-statistic): | 8.71e-05 |
| Time: | 11:37:49 | Log-Likelihood: | 102.77 |
| No. Observations: | 94 | AIC: | -193.5 |
| Df Residuals: | 88 | BIC: | -178.3 |
| Df Model: | 5 | ||
| Covariance Type: | nonrobust |
| coef | std err | t | P>|t| | [0.025 | 0.975] | |
|---|---|---|---|---|---|---|
| Intercept | 0.3206 | 0.021 | 15.231 | 0.000 | 0.279 | 0.362 |
| condition[T.После] | -0.0569 | 0.024 | -2.353 | 0.021 | -0.105 | -0.009 |
| mod[T.v] | -0.0486 | 0.025 | -1.964 | 0.053 | -0.098 | 0.001 |
| isi[T.4] | 0.0940 | 0.021 | 4.417 | 0.000 | 0.052 | 0.136 |
| isi[T.8] | 0.0639 | 0.021 | 3.026 | 0.003 | 0.022 | 0.106 |
| condition[T.После]:mod[T.v] | 0.0364 | 0.035 | 1.052 | 0.296 | -0.032 | 0.105 |
| Omnibus: | 7.764 | Durbin-Watson: | 1.631 |
|---|---|---|---|
| Prob(Omnibus): | 0.021 | Jarque-Bera (JB): | 12.254 |
| Skew: | 0.275 | Prob(JB): | 0.00218 |
| Kurtosis: | 4.681 | Cond. No. | 7.30 |
Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
anova_lm(mo)
| df | sum_sq | mean_sq | F | PR(>F) | |
|---|---|---|---|---|---|
| condition | 1.0 | 0.037600 | 0.037600 | 5.353142 | 0.023015 |
| mod | 1.0 | 0.020738 | 0.020738 | 2.952536 | 0.089259 |
| isi | 2.0 | 0.142876 | 0.071438 | 10.170697 | 0.000106 |
| condition:mod | 1.0 | 0.007779 | 0.007779 | 1.107480 | 0.295511 |
| Residual | 88.0 | 0.618104 | 0.007024 | NaN | NaN |
В последней колонке искомые p-values.
Чтобы понять, как работают линейные модели с категориальными факторами, отобразим матрицу дизайна. Все сочетания уровней действующих факторов кодируются сочетаниями нулей и единиц.
mo.model.exog_names
['Intercept',
'condition[T.После]',
'mod[T.v]',
'isi[T.4]',
'isi[T.8]',
'condition[T.После]:mod[T.v]']
figure(figsize=(8,8))
pcolor(mo.model.exog);
xticks(arange(6)+.5, mo.model.exog_names);

Для кодирования фактора с двумя уровнями достаточно одной колонки. Для кодирования МСИ с 3 уровнями задействованы две колонки: МСИ=2 кодируется двумя нулями в колонках для isi=4 и isi=8.
Групповые рисунки¶
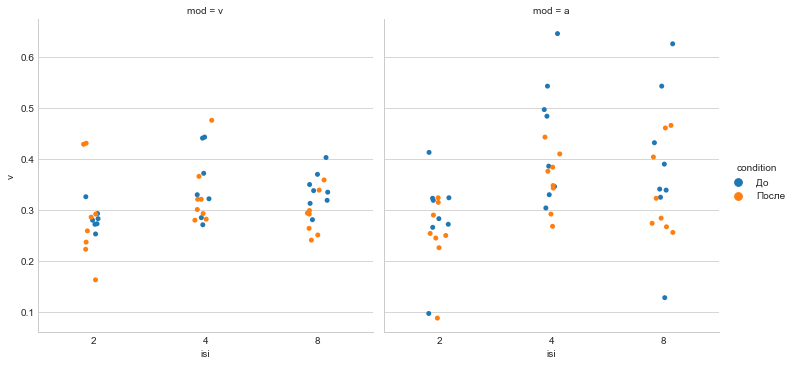
Для визуального сравнения групп между собой можно отображать как отдельные значения, так и расчётные параметры.
sns.catplot(x='isi', y='v', hue='condition', data=D, col='mod');
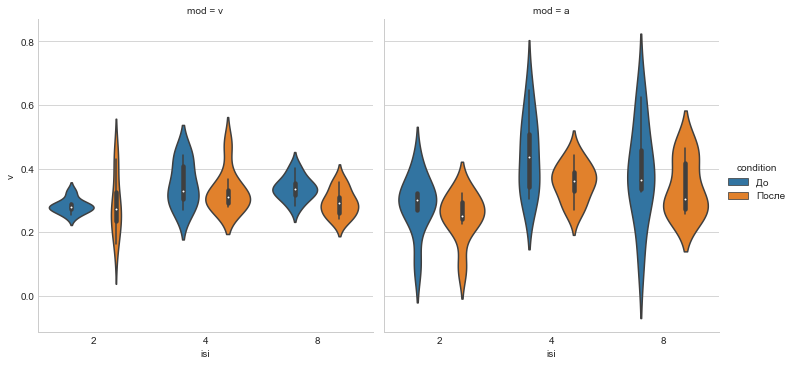
sns.catplot(x='isi', y='v', hue='condition', data=D, col='mod', kind='violin');
sns.catplot(x='isi', y='v', hue='condition', data=D, col='mod', kind='point');
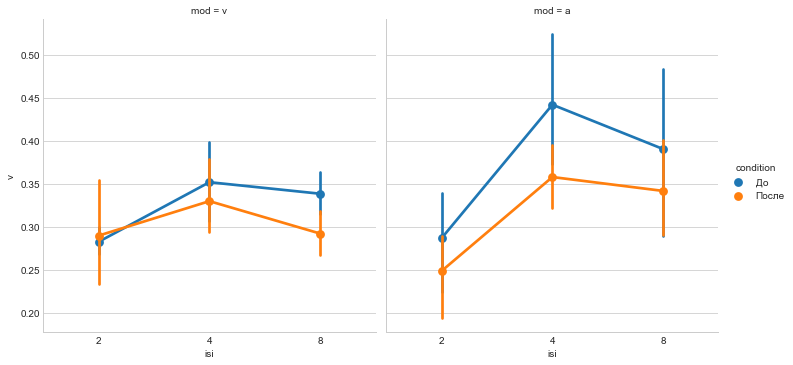
pal = {'До':'orange', 'После':'green'}
sns.catplot(x='isi', y='v', hue='condition', data=D, col='mod', kind='bar', palette=pal);
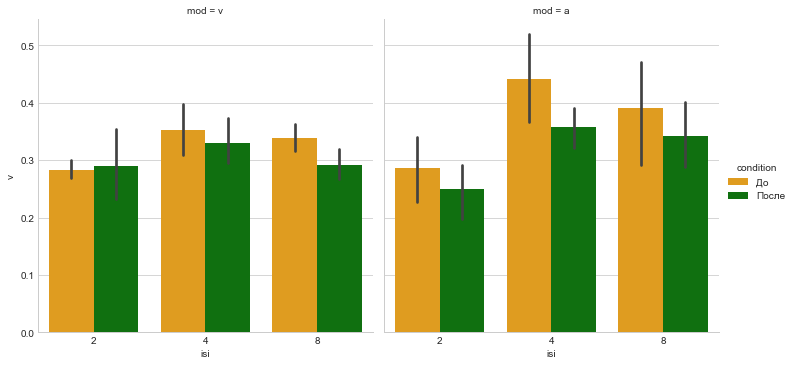
Разные типы рисунков подчеркивают различные аспекты соотношения между групповыми средними.
