Предсказание будущих реакций на основе предшествующих
Предсказание будущих реакций на основе предшествующих¶
Рассмотрим некоторые приемы прогнозирования на примере времен реакции в тесте «Баланс внимания».
u='http://balatte.stireac.com/result.tsv/masha7597%40gmail.com/125.62.117.87.donpac.ru__5122196921230210115'
D = pd.read_csv(u, delimiter='\t')
D.info()
<class 'pandas.core.frame.DataFrame'>
RangeIndex: 48 entries, 0 to 47
Data columns (total 2 columns):
# Column Non-Null Count Dtype
--- ------ -------------- -----
0 t 48 non-null float64
1 v 44 non-null float64
dtypes: float64(2)
memory usage: 896.0 bytes
sns.regplot(x='t',y='v',data=D); ylim(0);
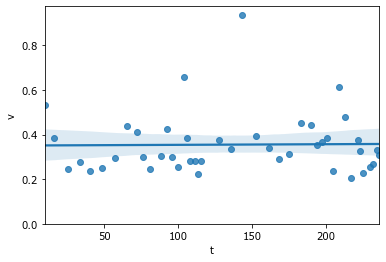
Представим, что мы хотим предсказывать время реакции (ВР) непосредственно в ходе эксперимента. Другими словами, мы хотим делать прогноз в режиме «реального времени».
Для упрощения представим, что мы ничего не знаем о заданном порядке МСИ и о модальности стимула.
В нулевой момент времени у нас нет данных. Мы прогнозируем, что ВР будет как у большинства людей от 150 до 350 мс. Возьмём среднее значение 0.25 с.
# заполним всю колонку этим значением
D['prognoz'] = 0.25
D.head()
| t | v | prognoz | |
|---|---|---|---|
| 0 | 9.675 | 0.535 | 0.25 |
| 1 | 16.331 | 0.383 | 0.25 |
| 2 | 25.539 | 0.246 | 0.25 |
| 3 | 33.650 | 0.279 | 0.25 |
| 4 | 40.687 | 0.235 | 0.25 |
Первые 9 секунд нашего эксперимента у нас все еще нет данных, и мы не можем оценить качество нашего прогноза. Как только появляются данные - мы можем рассчитать отклонение. Чтобы не зависеть от знака - среднеквадратичное отклонение (root-mean-square error (RMSE)).
sqrt(mean((D.v[0] - D.prognoz[0])**2))
0.28500000000000014
В случае одного значения это абсолютное значение разности между прогнозируемым и реальным значениями. Если значений много, то все равно будет одно число. Это число - метрика качества нашего прогноза, на основании которой мы можем сравнивать разные алгоритмы.
Есть несколько принципов прогноза:
Если что-то происходит сейчас так, то и в будущем будет так же.
Если есть четкая тенденция, то она продолжится.
Текущее значение может быть артефактом, т.е. возникло в результате случайного непредвиденного воздействия, которое больше может не повториться.
Чем больше данных в прошлом, тем лучше можно сделать прогноз будущего.
Мы попробуем сделать несколько логических шагов для понимания сути однонаправленного моделирования. Более зрелые модели доступны в специальных пакетах, на которые будут ссылки в конце.
#сохраним текущий прогноз как вариант подхода "среднее по больнице"
D['pro_populatio'] = D['prognoz']
#зададим функцию для удобства оценки качества прогноза
def quo(k):
'''чем больше отклонение - тем ниже эффективность'''
return 1/sqrt(mean((D.v - D[k])**2))
quo('pro_populatio')
5.907615132815684
Итого, если прогноз делать с потолка, то есть считать, что как у всех в среднем, то его эффективность 6 «попугаев».
Возьмем на вооружение первый принцип. Будем ждать каждый раз повторения последнего значения.
D.prognoz[1:]= D.v[:-1]
D.prognoz.fillna(method='ffill', inplace=True) #при пропусках оставляем предыдущий
D['pro_prev'] = D['prognoz']
quo('pro_prev')
5.486622605210117
Удивительно, но прогноз оказался хуже. Потому что постоянные 0.25 не так далеко от большинства значений в районе 0.3, а вот при прогнозе по предыдущему отдельные выбросы более 0.6 сделали свое черное дело: прогноз после них был крайне неудачным.
def play_prognoz(k='prognoz', n_future = 1, k0='v', interval=500):
xx=D.index.values
tt= xx[:-1]
fig = figure()
xlim(0,len(D.index)+1); ylim(0,0.7);
hh=[]
hh.append( plot([],[], color='b', lw=0, marker='d')[0] )
hh.append( plot(xx[0],D[k][0], color='r', marker='*')[0] ) #prognoz
hh.append( vlines([],[],[], colors='pink') ) #residuals
xlabel('Время, с');
ylabel('Интервал между нажатиями, с');
def updatefig(i):
hh[0].set_data(xx[:i+1], D[k0][:i+1])
hh[1].set_data(xx[[i,i+n_future]], D[k][[i,i+n_future]])
res1=vstack([tile(xx[i],(2,)), [D.loc[i,k0],D.loc[i,k]]]).T
hh[2].set_segments((hh[2].get_segments() + [res1]))
return hh
close()
ani = animation.FuncAnimation(fig, updatefig, tt, interval=interval, blit=True, repeat=False)
return ani #HTML(ani.to_html5_video())
play_prognoz('pro_prev')
Из-за выбросов становится понятно, что полагаться только на последнее значение опрометчиво. Лучше использовать для прогноза несколько последних значений.
Для ослабления влияния выбросов в качестве оценки центральной тенденции лучше использовать медиану.
D['pro_median5']=D.v.rolling(5, min_periods=1).median().shift()
play_prognoz('pro_median5')
Сравним эффективность предсказания по медиане с предсказанием по среднему.
D['pro_mean5']=D.v.rolling(5, min_periods=1).mean().shift()
quo('pro_median5'), quo('pro_mean5')
(6.804521891972025, 6.402599796091294)
И среднее, и медиана являются способами оценить центральную тенденцию (M-estimator)
Вместо усреднения можно ввести взвешенное среднее, чтобы более экстремальные значения вносили меньший вклад, чем более типичные близкие к среднему. На практике используются разные весовые функции. Например, после первых 5 значений мы хотели бы иметь прогноз в районе 0.3, т.е. ослабить влияние 4-го значения, превышающего 0.4.
x=D.v[:5]
z=((x - x.mean())/x.std()).values
z
wRamsay = exp(-0.3*abs(z)) #Ramsay’s Ea
wRamsay = wRamsay/sum(wRamsay)
t=1.345; wHuber = [(t/_z if _z>t else 1.) for _z in abs(z)]
wHuber = wHuber/sum(wHuber)
mean(x), sum(x*0.2), sum(x*wRamsay), sum(x*wHuber)
(0.3356000000000002,
0.3356000000000002,
0.32689472668338837,
0.3293876357432312)
Окна Рамсея и Хубера дали небольшое снижение относительно обычного среднего, в котором все слагаемые имеют одинаковый вес.
Мы берем 5 последних значений, значит средний возраст данных для прогноза - 3 временных шага. Получается, что если в серии происходят изменения - мы постоянно запаздываем в среднем на 3 шага назад.
Попробуем реализовать еще один принцип - недавние события имеют большую предсказательную силу, чем предыдущие. Для этого наделим большим весом последнее значение, а предыдущие - постепенно убывающими весами.
# weighted moving average (WMA)
w=(arange(5)+1)
w=w/w.sum()
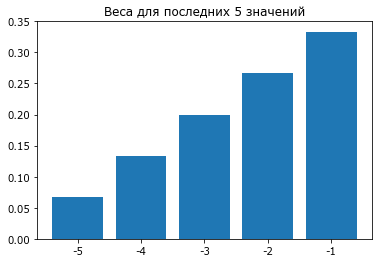
bar(arange(5), w); xticks(arange(5), -(5-arange(5)))
title('Веса для последних 5 значений');
rol = D.v.fillna(method='ffill').rolling(5)
D['pro_wma']=rol.apply(lambda x: sum(x*w[-len(x):])).shift() #shifts to future on 1 step
quo('pro_wma')
6.471412352935483
play_prognoz('pro_wma')
Последствия после выбросов сохраняются на несколько шагов.
Популярное решение - простое экспоненциальное сглаживание (simple exponential smoothing (SES)) или exponentially weighted moving average (EWMA).
# exponentially weighted moving average (EWMA)
alpha = 0.6
# (1 − α)2
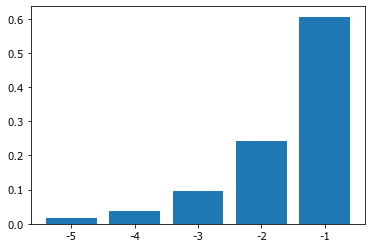
w=alpha*((1-alpha)**arange(5,0,-1))
w=w/w.sum()
bar(arange(5), w); xticks(arange(5), -(5-arange(5)));
rol = D.v.fillna(method='ffill').rolling(5)
D['pro_ewma']=rol.apply(lambda x: sum(x*w[-len(x):])).shift()
quo('pro_ewma')
6.173528063436437
play_prognoz('pro_ewma')
Используя экспоненциально взвешенную среднюю, мы еще меньше попугаев. Нам все еще мешают выбросы. Попробуем объединить веса, ослабляющие экстремальные значения, с весами, ослабляющими старые значения. Это так называемая конволюция.
def _conv1(x, alpha = 0.5):
wEWMA=alpha*((1-alpha)**arange(5,0,-1))
z=((x - x.mean())/x.std())
w = exp(-0.3*abs(z)) #Ramsay’s Ea
w=w*wEWMA
w = w/sum(w)
return sum(x*w)
_conv1(x)
0.26648572256798597
D['pro_conv1']=rol.apply(_conv1).shift()
quo('pro_conv1')
6.5133006602661485
play_prognoz('pro_conv1')
Если мы уверены, что величина выброса не имеет значения, то можем загнать данные в заданные рамки. Это позволит более адекватно оценивать модели. Просто удалить выбросы при моделировании динамики нежелательно, поскольку мы нарушим ход времени. Замена на пустые значения также снизит информативность.
Например, в данном случае что 0.45, что 0.65 с характеризуют поздние реакции при пропуске стимула. Мы можем задать границу 0.45, чтобы все поздние реакции отклонялись в большую сторону, но при этом не так влияли на среднее значение. Такой прием, автоматически загоняющий выбросы в пределы заданных перцентилей, называется винсоризацией.
import scipy.stats.mstats
D['vwin']=scipy.stats.mstats.winsorize(D.v, 0.2)
D.vwin.describe()
count 48.000000
mean 0.347125
std 0.076015
min 0.256000
25% 0.279750
50% 0.333000
75% 0.429750
max 0.453000
Name: vwin, dtype: float64
D['pro_win_conv']=D.vwin.fillna(method='ffill').rolling(5).apply(_conv1).shift()
quo('pro_win_conv')
6.9193910481797145
play_prognoz('pro_win_conv', k0='vwin')
Можно попробовать еще более продвинутые методы расчета весовых коэффициентов для подбора лучшего предсказания по группе последних значений, например IRLS с функцией потерь Хубера или разные варианты ARIMA.
Кроме линейной применяют более плавную сплайновую интерполяцию — scipy.interpolate.spline.
