Случайность - двигатель прогресса?
Случайность - двигатель прогресса?¶
Рассмотрим самый биологически успешный бинарный вероятностный процесс - разделение на два пола.
В статье из журнала «Reproduction in domestic animals» [HYF05] описан случай, когда небольшая популяция черных лебедей (Cygnus atratus) в неволе на Исследовательской базе разведения гигантских панд в Чэнду отказывалась размножаться в течение 4-5 лет. Была высказана гипотеза, что вероятной причиной этого является ненормальное распределение по полу.
Когда проверили - все 7 оказались самки. Проблема заключалась в том, что черный лебедь является примером сексуально мономорфных видов. Для определения пола пришлось разрабатывать метод, основанный на ПЦР.
pSex = 0.5
n = 7
Какая вероятность, что из 7 отобранных яиц вылупились все самки, если исходная вероятность рождения самки из яйца такая же, как и самца?
Поскольку события независимые, то вероятности нужно перемножать. Перемножение одинаковых вероятностей - это возведение в степень.
p7 = pSex**7
p7
0.0078125
Отношение одного исхода к другому называют шанс (odds).
odds = (1-p7)/p7
odds
127.0
Шансы, что так получилось случайно 1:127. Т.е. скорее всего повлиял какой-то фактор, вызвавший преобладание самок в выводке.
Какой должен быть процент самок в инкубаторе, чтобы чисто случайно можно было получить 7 самок из вытащенных наугад яиц? Шанс случайного исхода примем традиционный \(1:20\) , что соответствует уровню значимости 5%.
alpha=0.05
alpha**(1/7.0)
0.6518363448688391
Какое распределение полов следовало ожидать при таком проценте самок?
Проведем эксперимент с помощью генератора случайных чисел. Проверка гипотез путем многократной имитации исследуемого случайного процесса называется метод «Монте-Карло».
p=0.651836345
xx=arange(8)
P=zeros(8)
N=10000
for j in range(N):
n=0
for i in range(7):
if random.random() < p:
n+=1
P[n]+=1
bar(xx-0.5, P/N, width=1.0); xlabel('Количество самок в выборке');
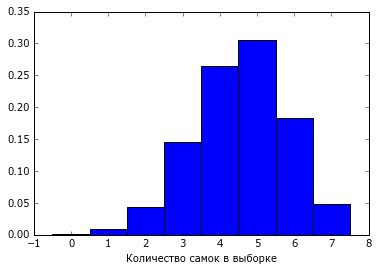
Конечно же существует специальная функция, которая генерирует случайную выборку с заданной долей одного вида объектов из двух возможных. Такое распределение называется биноминальное : bi - два, nomen - имя.
X = random.binomial(7, p, N) # посмотрите справку о порядке аргументов
hist(X, arange(-0.5,8), normed=True);
xlabel('Количество самок в выборке');
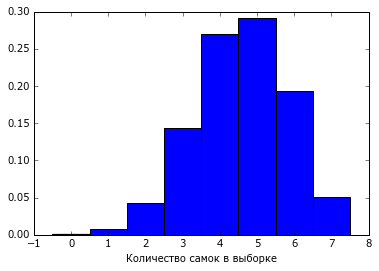
Как видно из рисунка, при таком приблизительно двухкратном преобладании самок, скорее всего было бы 5 самок и два самца. Могло бы быть и 4 или 6 самок. Но только в 1 из 20 случаев было бы 7 самок, и это как раз соответствовало бы заданному нами \(\alpha=0.05\).
Вот так из-за случайности зоологам пришлось разработать специальный метод определения пола лебедей.
Примечание
Чёрный лебедь - знаковое животное для теории вероятности. Именно этот эпитет используют для обозначения изначально невероятных, но вполне реальных значимых исходов.
После обнаружения живых черных лебедей этот термин стал использоваться для обозначения идеи о том, что воспринимаемая невозможность впоследствии может быть опровергнута.
Чёрные лебеди были, хотя цивилизованные люди существовали на земле три тысячи лет, не встречаясь с ними… Следовательно, единообразный опыт жителей известного мира, согласных в общем результате, без единого известного случая отклонения от этого результата, не всегда достаточен для установления общего вывода. John Stuart Mill, A System of Logic (1843)
Через опыт мы можем судить о ложности некоего высказывания, но никогда о его истинности Карл Поппер, Логика научного исследования (1934)
Отвергание нулевой гипотезы в классическом статанализе не означает подтверждение альтернативной гипотезы.
… должны ли мы на практике принимать единственный контрпример - например, одного обнаруженного черного лебедя - для опровержения весьма успешного закона. Я не полагаю, что мы должны обязательно так легко быть этим удовлетворены; мы вполне можем подозревать, что данный черный экземпляр перед нами не является лебедем. Карл Поппер, Логика научного исследования (1934)
Обычно исследователь свободен в удалении из выборки неудачных экспериментов (артефактов). На этом построен механизм умышленной дефальсификации: Систематическое исключение редких нежелательных явлений дает впечатление подтверждения однобокой теории.
См.также
Одноименную популярную теорию развил Нассим Николас Талеб. В своих работах он описывает случаи, когда выбросы имеют важное значение (статистики говорят: в распределении «жирные хвосты» (fat tails)). В этом случае общепринятые статистические законы не работают.
