Проверка нормальности распределения
Проверка нормальности распределения¶
Загрузим данные - время реакции, с.
D = pd.read_table('d/rt.tsv')
vv=D.v.dropna()
hist(vv); xlabel('время реакции, с');
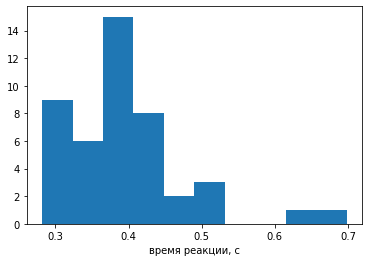
Стандартная проверка - по статистике хи-квадрат, комбинирующей z-тесты асимметрии и куртозиса.
import scipy.stats as stats
stats.normaltest(vv)
NormaltestResult(statistic=19.306090837311295, pvalue=6.422966266742602e-05)
p очень маленькое, значит отвергаем гипотезу о нормальности распределения. Увы, распределение ВР почти всегда скошено вправо.
Более мощный тест (по мнению некоторых источников) - Шапиро-Уилка (Shapiro-Wilk). Подходит для небольших выборок.
stats.shapiro(vv)
ShapiroResult(statistic=0.8942419290542603, pvalue=0.0006301295361481607)
p-value на порядок больше.
Тест Колмогорова-Смирнова может быть применен более широко, чем Шапиро, поскольку он сравнивает любые два распределения друг с другом, а не обязательно с нормальным. Для правильного использования необходимо z-преобразование.
zz=(vv-vv.mean())/vv.std()
stats.kstest(zz, cdf='norm')
KstestResult(statistic=0.1330234060534219, pvalue=0.37054082680262057)
Еще есть тест Андерсона - вариант теста Колмогорова-Смирнова.
stats.anderson(vv)
AndersonResult(statistic=1.0696390939463, critical_values=array([0.535, 0.609, 0.731, 0.853, 1.014]), significance_level=array([15. , 10. , 5. , 2.5, 1. ]))
Только последние два теста на 5% уровне значимости показали, что распределение можно считать нормальным.
Попробуем убрать выбросы более .5 с из набора данных.
vv_ = vv[vv<0.5]
print(f'изменение размера {len(vv)} -> {len(vv_)}')
изменение размера 45 -> 40
stats.normaltest(vv_)
NormaltestResult(statistic=2.25019618656403, pvalue=0.3246206226942116)
stats.shapiro(vv_)
ShapiroResult(statistic=0.9592655301094055, pvalue=0.15807799994945526)
stats.kstest((vv_-vv_.mean())/vv_.std(), cdf='norm')
KstestResult(statistic=0.10612495428368313, pvalue=0.7187460361580543)
stats.anderson(vv_)
AndersonResult(statistic=0.47606646495707139, critical_values=array([ 0.531, 0.605, 0.726, 0.847, 1.007]), significance_level=array([ 15. , 10. , 5. , 2.5, 1. ]))
Вывод: после удаления выбросов можно использовать параметрические методы для анализа ВР.
