Скрининговая диагностика
Содержание
Скрининговая диагностика¶
Данные по маммографии - один из общедоступных наборов данных в архиве Центра машинного обучения. Собран в Институте Радиологии университета Эрланген-Нюрнберг, Erlangen, Germany в период между 2003 и 2006 гг [ESWW07].
Маммография является наиболее эффективным методом скрининга рака молочной железы, доступным сегодня. Однако низкая положительная прогностическая ценность биопсии молочной железы в результате интерпретации маммографии приводит к примерно 70% ненужных биопсий с доброкачественными результатами. Для снижения количества ненужных биопсий молочных желез предлагаются системы автоматизированной диагностики, которые помогают врачу решить: делать биопсию подозрительного участка или пока отложить инвазивную проверку и понаблюдать.
Колонки:
Оценка BI-RADS в диапазоне от 1 (определенно доброкачественная) до 5 (очень подозрительно злокачественная), полученная в процессе двойного осмотра врачами. (порядковый)
Возраст пациента в годах
Форма образования: round=1 oval=2 lobular=3 irregular=4
Край образования: очерченный = 1 мелкодольчатый = 2 расплывчатый = 3 плохо определенный = 4 пальчатый = 5
Плотность образования: высокая = 1 изо = 2 низкая = 3 жиросодержащая = 4 (порядковый)
Реальная тяжесть: доброкачественная = 0 или злокачественная = 1 (биноминальный)
#https://archive.ics.uci.edu/ml/machine-learning-databases/mammographic-masses/mammographic_masses.data
kk = 'est age forma krai dens itog'.split()
D = pd.read_csv('d/mammographic_masses.data', names=kk, header=None, na_values='?')
D.info()
<class 'pandas.core.frame.DataFrame'>
RangeIndex: 961 entries, 0 to 960
Data columns (total 6 columns):
# Column Non-Null Count Dtype
--- ------ -------------- -----
0 est 959 non-null float64
1 age 956 non-null float64
2 forma 930 non-null float64
3 krai 913 non-null float64
4 dens 885 non-null float64
5 itog 961 non-null int64
dtypes: float64(5), int64(1)
memory usage: 45.2 KB
Создайте ячейку и, выполнив код
D, посмотрите содержимое таблицы. Возьмите одну строчку и объясните ситуацию у данного пациента.
# D.loc[562]
Посмотрим распределение всех четырех объясняющих показателей. При этом настроим палитру, чтобы плохой исход был пугающе красным, а хороший - успокаивающе зеленым. (n=2)
#pal = sns.choose_diverging_palette()
pal = sns.diverging_palette(120, 350, n=2, sep=10)
sns.color_palette(pal)
sns.pairplot(data=D, x_vars=D.columns[:-1], y_vars=D.columns[:-1], dropna=False,
hue="itog",
diag_kind="kde",
palette=pal);
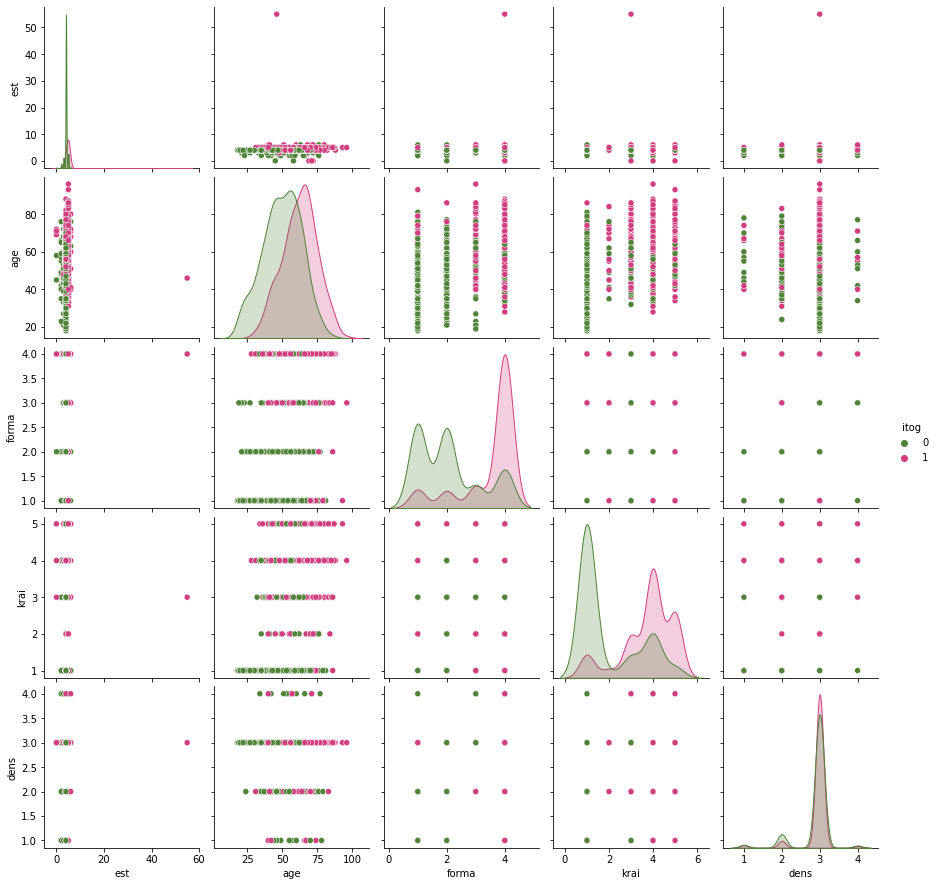
Видны расхождения по многим признакам, а значит можно настроить прогностическую модель, которая будет предсказывать итог.
Авторами заявлено, что оценка врачей est варьирует от 1 до 5. Одно значение 55. Это явно опечатка.
D.loc[D.est>5,'est']=5
D.loc[D.est<1,'est']=1
D.hist('est');
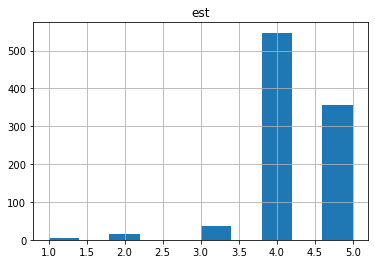
Могли ли врачи предсказать итоги биопсии?
(
D.est.corr(D.itog),
D.est.corr(D.itog, 'kendall'),
D.est.corr(D.itog, 'spearman')
)
(0.5360230051347603, 0.6061147157824877, 0.6213620971586996)
Оценки врачей коррелировали с итоговыми данными биопсии.
Зависимость от возраста¶
Чем старше возраст пациентки, тем больше вероятность того, что образование злокачественное.
D.plot('age','itog', kind='scatter', alpha=.5);
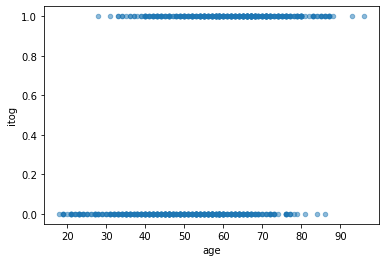
Диапазоны значительно перекрываются и, например, нельзя однозначно сказать о качестве новообразований у женщин в возрасте 50 лет. Поскольку исходов всего два, то можно говорить о вероятности.
Давайте преобразуем данные в вероятности - доли одного исхода события от общего количества событий.
D.age.hist(bins=25);
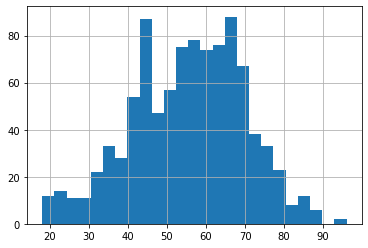
Следует отметить, что сходство распределения по возрасту с нормальным распределением говорит не о законе распределения признака (как известно возраст начинается с 0), а лишь о том, в каком возрасте у женщин встречаются образования в грудных железах.
Давайте поделим весь диапазон на пятилетки и посчитаем процент злокачественности.
agegroup = np.arange(15,105,5)
D['agegroup'] = pd.cut(D.age, agegroup)
D.groupby(['agegroup']).itog.count()
agegroup
(15, 20] 6
(20, 25] 23
(25, 30] 19
(30, 35] 44
(35, 40] 58
(40, 45] 94
(45, 50] 96
(50, 55] 111
(55, 60] 139
(60, 65] 114
(65, 70] 108
(70, 75] 67
(75, 80] 49
(80, 85] 15
(85, 90] 11
(90, 95] 1
(95, 100] 1
Name: itog, dtype: int64
Самыми многочисленными оказались возрастные группы от 50 до 70 лет.
Наша задача сгруппировать женщин по двум колонкам и посчитать количество случаев принадлежности к группам в одной и другой колонках.
G = D.groupby(['agegroup','itog']).itog.count().unstack()
G
| itog | 0 | 1 |
|---|---|---|
| agegroup | ||
| (15, 20] | 6 | 0 |
| (20, 25] | 23 | 0 |
| (25, 30] | 18 | 1 |
| (30, 35] | 38 | 6 |
| (35, 40] | 44 | 14 |
| (40, 45] | 66 | 28 |
| (45, 50] | 65 | 31 |
| (50, 55] | 64 | 47 |
| (55, 60] | 77 | 62 |
| (60, 65] | 53 | 61 |
| (65, 70] | 34 | 74 |
| (70, 75] | 14 | 53 |
| (75, 80] | 11 | 38 |
| (80, 85] | 2 | 13 |
| (85, 90] | 1 | 10 |
| (90, 95] | 0 | 1 |
| (95, 100] | 0 | 1 |
Заменим отсутствующие значения и подсчитаем общее количество.
G = G.fillna(0).astype(int)
G = G.rename(columns={0:'dobro', 1:'zlo'})
G['N'] = G.dobro + G.zlo
G
| itog | dobro | zlo | N |
|---|---|---|---|
| agegroup | |||
| (15, 20] | 6 | 0 | 6 |
| (20, 25] | 23 | 0 | 23 |
| (25, 30] | 18 | 1 | 19 |
| (30, 35] | 38 | 6 | 44 |
| (35, 40] | 44 | 14 | 58 |
| (40, 45] | 66 | 28 | 94 |
| (45, 50] | 65 | 31 | 96 |
| (50, 55] | 64 | 47 | 111 |
| (55, 60] | 77 | 62 | 139 |
| (60, 65] | 53 | 61 | 114 |
| (65, 70] | 34 | 74 | 108 |
| (70, 75] | 14 | 53 | 67 |
| (75, 80] | 11 | 38 | 49 |
| (80, 85] | 2 | 13 | 15 |
| (85, 90] | 1 | 10 | 11 |
| (90, 95] | 0 | 1 | 1 |
| (95, 100] | 0 | 1 | 1 |
Считаем вероятность…
G['p'] = G.zlo/G.N
G.p.plot(kind='area', color='maroon', ylim=(0,1));
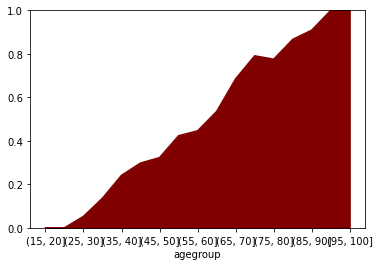
Похоже на линейную зависимость вероятности от возраста. Но линейный тренд будет продолжаться вверх и вниз, а вероятность не может быть 120% в возрасте 110 лет или -10% в возрасте 10 лет. Адекватная модель должна попадать только в диапазон [0, 1].
Нам подходит логистическая модель, описывающая переход от 1 к 0 или обратно.
import scipy.optimize as optimize
def func(x, x0, k):
# '''https://en.wikipedia.org/wiki/Logistic_function'''
return 1 / (1 + np.exp(k*(x-x0)))
# Чтобы попасть в середину пятилетних диапазонов, то к нижним границам
# надо прибавить половину диапазона - 2.5 года.
x = agegroup[:-1] + 2.5
y = G.p.values
# добавим полочки, чтобы подбор модели был надежным
yopt = r_[[0,0,0], y, [1,1,1]]
xopt = np.arange(0,115,5) + 2.5
popt, pcov = optimize.curve_fit(func, xopt, yopt,
# bounds=([20, -1], [90, 0]),
p0=[55, 0])
popt
array([57.68166044, -0.0779198 ])
Чтобы оценить подгонку модели, наложим полученную кривую на исходные значения вероятности.
Для оценки надежности эмпирической вероятности можно посчитать доверительный интервал, но алгоритм для этого должен быть особый - ведь границы интервала не должны выходить за пределы диапазона [0…1].
from statsmodels.stats.proportion import proportion_confint
lower, upper = proportion_confint(G.zlo, G.N, 0.05)
co='b'
plot(x, y, marker='o', lw=0, color=co, alpha=.8, zorder=3, label='% злокач.')
# добавим доверительные интервалы
plot(np.tile(x, (2,1)), c_[lower, upper].T, co)
xx = linspace(x.min(), x.max(), 200)
yy = func(xx, *popt)
plot(xx, yy, color='m', ls='-', zorder=10, label='модель');
axvline(popt[0], color='k', ls='--', alpha=.8, label='перелом')
axhline(0, color='k', ls='-', lw=1, alpha=.6)
axhline(1, color='k', ls='-', lw=1, alpha=.6)
xlabel('Возраст');
ylabel('Вероятность')
legend();
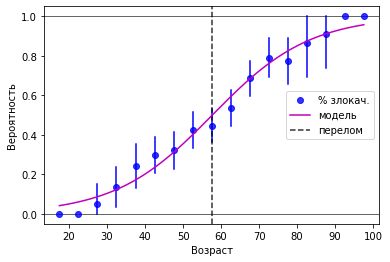
Вывод. После 58 лет преобладает вероятность злокачественного исхода новообразований в груди.
Мы использовали огрубленные данные, поскольку считали вероятности с шагом в 5 лет. А что, если попробовать подобрать логистическую модель к исходным данным без подсчета вероятности?
D_ = D[D.age.notnull()] #отберем только с указанием возраста
x = D_.age
y = D_.itog
# зададим в качестве начальных значений полученные ранее
popt, pcov = optimize.curve_fit(func, x, y, p0=[50, -0.07])
popt
array([58.52211327, -0.07062092])
Стандартную ошибку получаем как корень квадратный из вариаций, которые идут по диагонали ковариационной матрицы.
perr = np.sqrt(np.diag(pcov))
perr
array([0.98835055, 0.00662141])
D.plot('age','itog', kind='scatter', alpha=.5, label='данные');
xx = linspace(x.min(), x.max(), 200)
yy = func(xx, *popt)
plot(xx,yy, color='m', ls='-', zorder=10, label='модель');
yymax = func(xx, *(popt+perr))
yymin = func(xx, *(popt-perr))
fill_between(xx, yymin, yymax, alpha=0.1, color='m')
axvline(popt[0], color='k', ls='--', alpha=.8, label='перелом')
axhline(0.5, color='k', ls='-', lw=1, alpha=.6)
xlabel('Возраст');
ylabel('Злокачественность')
legend();
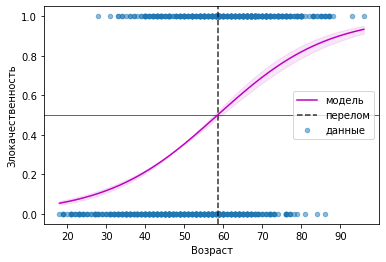
Вывод. Параметры логистической модели можно получить на выборке бинарных данных: из 0 и 1.
После 58.5 лет преобладает вероятность злокачественного исхода новообразований в груди.
