Преобразование данных в логарифмической шкале
Преобразование данных в логарифмической шкале¶
Логарифм - это степень, в которую надо возвести основание, чтобы получить аргумент. Т.е. логарифмирование является противоположной операцией возведению в степень.
Возведение в степень с любым основанием можно преобразовать в степень числа \(e\).
exp(1)
2.718281828459045
Поскольку обратной функцией к экспоненте является натуральный логарифм, то данные можно преобразовывать в одном направлении (потенцировать) и в обратном (логарифмировать) без потери соотношений в ряду данных.
x = arange(7)
vvE = exp(x) #экспоненциальная функция
vvElog = log(vvE)
plot(x, vvElog,'r^-', label='log(exp(x))')
vvlog = log(x[1:])
plot(x[1:], vvlog+1, 'mv:', label='log(x)+1');
plot(x[1:], exp(vvlog),'kx--', label='exp(log(x)+1)');
legend();
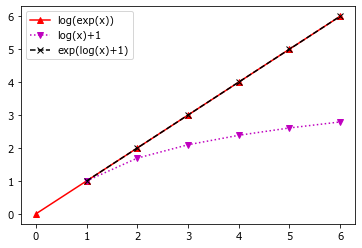
Как следует из легенды к рисунку - порядок обратных операций может быть любым.
Логарифм 0 даёт минус бесконечность (-Inf) (деление на 0).
log(0)
<ipython-input-4-2e1b7d281bdf>:1: RuntimeWarning: divide by zero encountered in log
log(0)
-inf
Чтобы использовать логарифмирование с данными, в которых есть нулевые значения, используют прибавление единицы, а при потенцировании таких данных - отнимание.
x = arange(7)
vvlog = log1p(x)
plot(x, vvlog, 'mv:', label='log(x+1)');
plot(x, expm1(vvlog),'ko--', label='exp(log(x+1))-1');
legend();
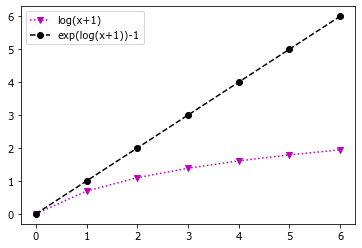
Сравним форму облаков распределения значений ВР от МСИ при представлении в разных шкалах.
lps=loadtxt('d/rt.tsv', skiprows=1)
lps.shape
(48, 2)
tt=lps[:,0]
isi=diff(tt)
vv=lps[1:,1]
plot(isi,vv,'o')
xlabel('МСИ, c')
xlim([0, 10]);
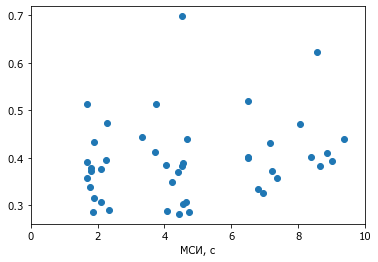
В соответствии со схемой теста три группы точек сгруппированы около 2, 4 и 8.
plot(log2(isi), log(vv), 'o')
xlabel('log(МСИ), у.е.')
xlim([0,4]);
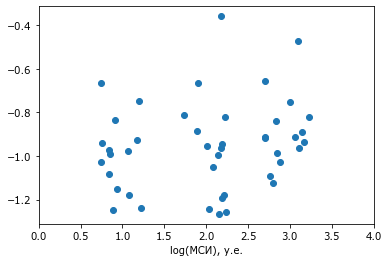
Можно заметить, что во втором случае облака точек выглядят более однородно и обособленно. Величины, указанные по обеим шкалам, стало труднее интерпретировать, потому что это логарифм от первоначальных шкал. Однако, к исходным величинам можно вернуться с помощью потенцирования.
