Содержание

Разведочный анализ утомленных лекцией

Разведочный анализ утомленных лекцией

Пример анализа данных, полученных в рамках проектной деятельности с помощью онлайн-приложения «Баланс внимания».

Методика

1-й этап эксперимента:

  • Подготовка испытуемого и настрой на проведение контрольного теста. - 10 минут

  • Контрольный тест баланса внимания #1. - 5 минут - Тест в обычных условиях без физических и умственных нагрузок

  • Отдых. - 7 минут

2-й этап эксперимента:

  • Воздействие на испытуемого умственной нагрузкой, понижающей мотивацию, в виде просмотра видеозаписи лекции на сложную и непонятную испытуемым тему ( лекция теории Марковских случайных процессов https://www.youtube.com/watch?v=UveMw1SjEM4 ) - 15 минут. Контроль внимательности просмотра видео обеспечивается путем подсчета количества произношения разных форм слова «процесс». (Например: процессом, процесса и т.д.)

  • Тест баланса внимания #2. - 5 минут

D = pd.read_table('d/rt9x2.tsv')
D
t v isi g mod subj cond nagr10
0 9.537 0.332 NaN 8.0 v 0 0 NaN
1 17.354 0.243 7.817 8.0 v 0 0 1.0
2 25.094 0.238 7.740 8.0 v 0 0 2.0
3 32.211 0.298 7.117 8.0 v 0 0 2.0
4 39.839 0.253 7.628 8.0 v 0 0 2.0
... ... ... ... ... ... ... ... ...
859 232.453 0.361 2.322 2.0 a 9 lect 4.0
860 234.724 0.298 2.271 2.0 a 9 lect 5.0
861 236.662 0.304 1.938 2.0 a 9 lect 5.0
862 239.017 0.309 2.355 2.0 a 9 lect 5.0
863 240.979 0.290 1.962 2.0 a 9 lect 5.0

864 rows × 8 columns

  • t время предъявления стимула, с

  • v время реакции, с

  • isi межстимульный интервал (МСИ), с

  • g режим стимуляции. В ходе тестирования МСИ задавался с небольшой вариацией в окрестности трех значений: 8, 4, 2 с. 8 - субъективно медленно, 4 - комфортно, 2 - часто. Функциональное состояние изменялось от монотонии до активации

  • mod модальность стимула visual - зрительный audial - слуховой

  • subj идентификатор участника

  • cond условие тестирования 0 - контроль, lect - после лекции

  • nagr10 - «текущая нагрузка» - количество стимулов, требующих реакции, за последние 10 с.

Проверка полноты выборки необходима, чтобы при всех сочетаниях факторов объём данных был достаточным для статистики. Проверка полноты выполняется путем подсчета значений в каждой группе.

D.groupby(['subj','cond','mod']).v.count()

subj  cond  mod
0     0     a      24
            v      24
      lect  a      24
            v      22
1     0     a      24
            v      23
      lect  a      24
            v      21
3     0     a      24
            v      24
      lect  a      24
            v      24
4     0     a      24
            v      23
      lect  a      24
            v      24
5     0     a      24
            v      23
      lect  a      24
            v      23
6     0     a      24
            v      21
      lect  a      24
            v      24
7     0     a      24
            v      23
      lect  a      19
            v      24
8     0     a      24
            v      24
      lect  a      24
            v      20
9     0     a      23
            v      24
      lect  a      24
            v      24
Name: v, dtype: int64

При группировке по нескольким колонкам на выходе получаем серию значений (pd.Series) со сложным индексом. У каждого значения в серии несколько указателей - по одному из каждой группирующей колонки. По первому индексу subj понятно, что в тесте приняли участие 9 субъектов (респондентов). В норме в каждой группе по 24 значения, но если были пропуски (значения отсутствуют), то в группе оказывается меньше значений.

Так как серия с количеством значений была на выходе последней команды, то к ней можно обратиться через специальное имя _ (подчерк). Например, узнать в какой группе было больше всего пропусков, и, соответственно, меньше всего числовых значений.

_.argmin()

26

Строка в таблице для значения может быть, а само значение в этой строке отсутствовать. В этом случае обычно на его месте ставят NaN (Not a Number).

D.v.isnull().sum()

23

Во всем наборе данных 23 пустых значения.

D.shape

(864, 8)

24 * 2 * 2 * 9  # n * mod * cond * subj

864

Таким образом, в таблице есть строчки для всех сочетаний факторов, но из-за пропусков реальных значений меньше. Анализ полноты повторных измерений (repeated measures) показал, что для каждого сочетания факторов было не менее 19 повторов.

Анализ распределения зависимой переменной

Зависимая переменная v - ВР, с.

Перед тем, как применять методы параметрической статистики нужно убедиться, что значения варьируют близко к нормальному распределению.

sns.histplot(D.v.dropna(), kde=True, element="step", label='Плотность');
axvline(D.v.median(),c='r',ls='--', label='Медиана');
xlabel('ВР, с')
ylabel('%')
legend();
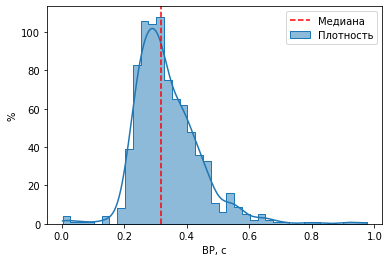
_images/i_anova_16_0.png

Распределение имеет четко выраженную центральную тенденцию - один «горб» посередине и плавно убывающие «хвосты» по бокам. Левый фронт более крутой - распределение асимметрично со сдвигом вправо. Для введения в модель степени асимметричности нужен еще один параметр, однако такое усложнение потребует специальных методов статистического анализа. В данном случае выгоднее пренебречь небольшим отклонением от нормальности в виде асимметрии, но при этом воспользоваться хорошо разработанным математическим аппаратом вариационной статистики.

Чтобы не влияли редкие значения, попавшие в хвосты распределения, «обрежем» его в тех границах, где плотность подходит к нулю.

X = D[(D.v>=.18)&(D.v<.72)]

В этом распределены смешаны данные, полученные при разных условиях и модальности стимулов. Сопоставим групповые выборки с помощью разных типов графиков.

sns.boxplot(x='cond', y='v', hue='mod', data=X, notch=True);
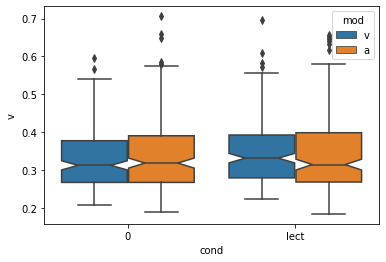
_images/i_anova_21_0.png 
sns.catplot(x='cond', y='v', hue='mod', data=X, kind='violin');
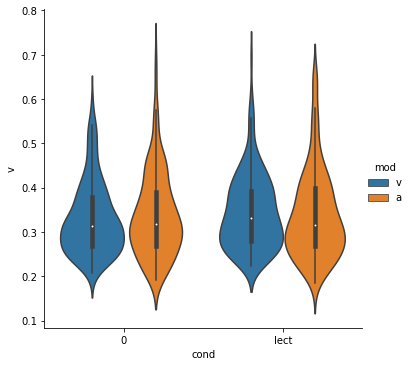
_images/i_anova_22_0.png

Вариационный анализ

Семейство статистических методов, оценивающих возможности объяснить дисперсию (вариацию) в целевом (зависимом) показателе за счет вариации объясняющих (независимых) показателей, называют дисперсионный анализ или анализ вариации. В названии конкретных методов часто встречается аббревиатура ANOVA (ANalysis Of VAriation). Основы дисперсионного анализа были разработаны Р. Фишером.

При записи формулы многофакторных моделей объясняющие факторы записывают как части суммы, а если еще учитывают их совместное (сочетанное) действие, то как множители произведения.

\[v \sim Cond*Mod\]

В процессе анализа основное внимание сосредоточим на действии фактора «условие» (cond), при этом разделяя реакции на стимулы разных модальностей (mod) - зрительные и слуховые, - потому что зрительное и слуховое внимание работают на основе разных механизмов.

Проведем многофакторный вариационный анализ для повторных измерений с помощью пакета statmodels.

mo = smf.mixedlm('v ~ cond*mod', data=X, groups='subj').fit()
mo.summary()

c:\a\winpython\python-3.9.0rc1.amd64\lib\site-packages\statsmodels\regression\mixed_linear_model.py:2237: ConvergenceWarning: The MLE may be on the boundary of the parameter space.
  warnings.warn(msg, ConvergenceWarning)
Model: MixedLM Dependent Variable: v
No. Observations: 824 Method: REML
No. Groups: 9 Scale: 0.0045
Min. group size: 88 Log-Likelihood: 1023.8836
Max. group size: 95 Converged: Yes
Mean group size: 91.6
Coef. Std.Err. z P>|z| [0.025 0.975]
Intercept 0.339 0.022 15.444 0.000 0.296 0.382
cond[T.lect] 0.002 0.007 0.316 0.752 -0.011 0.015
mod[T.v] -0.009 0.007 -1.305 0.192 -0.021 0.004
cond[T.lect]:mod[T.v] 0.011 0.009 1.143 0.253 -0.008 0.029
subj Var 0.004 0.031

Значения ВР в с слишком маленькие, и алгоритм подбора параметров модели выдает предупреждение о сходимости (ConvergenceWarning).

Попробуем перевести значения в мс и запустим еще раз.

D['rtms'] = D.v * 1000
X = D[(D.v>=.18)&(D.v<.72)]
mo = smf.mixedlm('rtms ~ cond*mod', data=X, groups='subj').fit()
mo.summary()
Model: MixedLM Dependent Variable: rtms
No. Observations: 824 Method: REML
No. Groups: 9 Scale: 4496.2534
Min. group size: 88 Log-Likelihood: -4640.4757
Max. group size: 95 Converged: Yes
Mean group size: 91.6
Coef. Std.Err. z P>|z| [0.025 0.975]
Intercept 338.706 21.932 15.444 0.000 295.721 381.691
cond[T.lect] 2.075 6.563 0.316 0.752 -10.789 14.938
mod[T.v] -8.560 6.562 -1.305 0.192 -21.421 4.300
cond[T.lect]:mod[T.v] 10.693 9.352 1.143 0.253 -7.636 29.021
subj Var 4138.924 31.394

В таблице результатов надо смотреть колонку P>|z| - это и есть p-value, вероятность того, что влияние факторов случайно. Действие фактора расценивается существенным, если p-значение меньше 0.05.

Если не учитывать ритм подачи стимулов, то различия не обнаруживаются.

Распределения с учетом МСИ

Если мы хотим сопоставить на одном рисунке несколько распределений, то вместо классических гистограмм, которые будут закрывать друг друга при наложении, можно использовать графики оценки плотности ядра (KDE - kernel density estimation).

График оценки плотности ядра (KDE) - это метод визуализации распределения наблюдений в наборе данных, аналогичный гистограмме. KDE представляет данные с использованием непрерывной кривой плотности вероятности.

g_lw = {2:3, 4:1.5, 8:0.8}
co_cond = {'0':'green', 'lect':'crimson'}

fig,ax = subplots(1,2, sharey=True, figsize=(12,6))

for i,modality in enumerate(['v','a']):
    sca(ax[i])
    title(modality)
    
    g=D[D['mod']==modality].groupby(['cond','g'])
    for k in sorted(g.groups.keys()):
        vv = g.get_group(k).v.dropna()
        cond,gr = k
        sns.kdeplot(vv, label=k, color=co_cond[cond], lw=g_lw[gr]);
    xlabel('ВР, с')
    ylabel('%')
    legend();
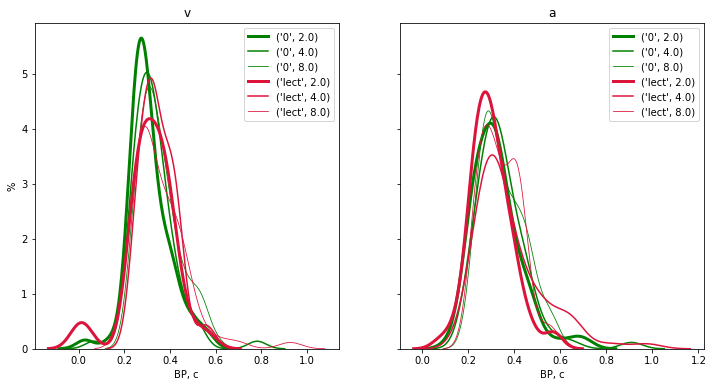
_images/i_anova_32_0.png

Фактор g - группа влияет достоверно, но как именно? И у всех ли испытуемых однонаправленно?

Анализ на R

Статистики исторически любят работать в среде языка R, поэтому самые свежие версии алгоритмов анализа могут быть доступны в виде библиотек на R. Если на компьютере установлен бесплатный пакет R, то тут же в блокноте можно провести анализ. Для этого надо загрузить расширение для подключения R.

%load_ext rpy2.ipython

После этого, если ячейка начинается со специальной команды %%R, то код в ней обрабатывается не в Python, а в R. Например, импорт библиотек на языке R осуществляется командой library, а не import.

%%R 
library(car)
library(lme4)

Для анализа нужно передать в среду R наш набор данных, который мы указываем после ключа -i - input вход.

%%R -i X

(m1 <- lmer(v ~ cond*mod*g + (1|subj), data = X))
Anova(m1, test.statistic="F")

На выходе получаем результат в виде текста:

Analysis of Deviance Table (Type II Wald F tests with Kenward-Roger df)

Response: v
                 F Df Df.res    Pr(>F)    
cond        2.5504  1 808.01    0.1107    
mod         0.5121  1 808.03    0.4745    
g          19.7105  1 808.02 1.026e-05 ***
cond:mod    1.5166  1 808.02    0.2185    
cond:g      1.8920  1 808.01    0.1694    
mod:g       0.6344  1 808.01    0.4260    
cond:mod:g  0.4963  1 808.02    0.4813    
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Значимость влияния фактора в результатах анализа помечены кодами - звёздочками. Чем больше звездочек, тем больше значимость.

Сопоставив средние ВР для трех МСИ, мы можем понять, что ВР при увеличении МСИ растет. В данном случае взаимодействие фактора g с другими не выявлено.

Чтобы оценить форму зависимости при разных сочетаниях уровней факторов, выведем график зависимости для каждого респондента.

h = sns.catplot(x='g', y='v', hue='subj', col='cond', row='mod', data=X, 
                   kind='point', alpha=0.5);
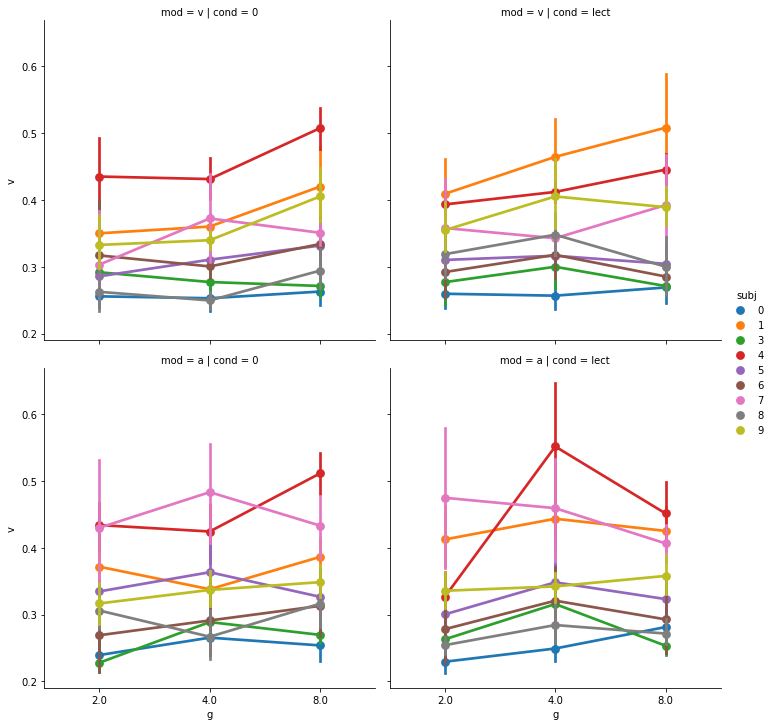
_images/i_anova_37_0.png

На одном рисунке мы визуализировали зависимости ВР от МСИ для каждой группы модальности/условия/испытуемого.

назад

Объединение наборов данных

вперёд

🗎 Сравнение выборок