Спектральный анализ
Спектральный анализ¶
Пример выделения частотных формантов из записи нашей местной райской птички. (Автор исходной записи уже удалился, но есть похожая запись). Копия оригинала.
Подготовительные операции (их можно автоматизировать, но здесь описывается ручной режим)
Скачать видео и извлечь из него аудио, или сразу скачать аудио (если получится). Не забывайте о соблюдении авторских прав. Должно быть разрешение автора.
Преобразовать аудио в формат WAV 16-bit PCM - колебания в диапазоне
[-32768 +32767]
Информация об аудио дорожке в видеофайле.
Audio
ID : 2
Format : AAC
Format/Info : Advanced Audio Codec
Format profile : LC
Codec ID : 40
Duration : 19s 202ms
Bit rate mode : Variable
Bit rate : 96.0 Kbps
Maximum bit rate : 102 Kbps
Channel count : 2 channels
Channel positions : Front: L R
Sampling rate : 44.1 KHz
Compression mode : Lossy
Stream size : 225 KiB (26%)
Title : IsoMedia File Produced by Google, 5-11-2011
Encoded date : UTC 2015-03-13 13:52:49
Tagged date : UTC 2015-03-13 13:52:49
u='d/merops.wav'
fs,y = wavfile.read(u)
y.shape
(846848, 2)
Запись открылась в виде 2-х длинных последовательностей чисел - левый и правый стереоканалы.
Посмотрите значение в переменной
fs. Убедитесь, что Вы четко понимаете, что характеризует частота оцифровки звука.
Для расчета продолжительности записи в секундах разделим длину последовательности на частоту в переменной fs
tmax=y.shape[0]/fs
tmax
19.202902494331067
Рассмотрим данные на рисунке. Также отобразим графически разницу между каналами.
fig, ax = subplots(3,1, figsize=(12,6), sharex=True)
x = arange(len(y))/fs
ax[0].plot(x,y[:,0]);
ax[1].plot(x,y[:,1]);
ax[2].plot(x,diff(y));
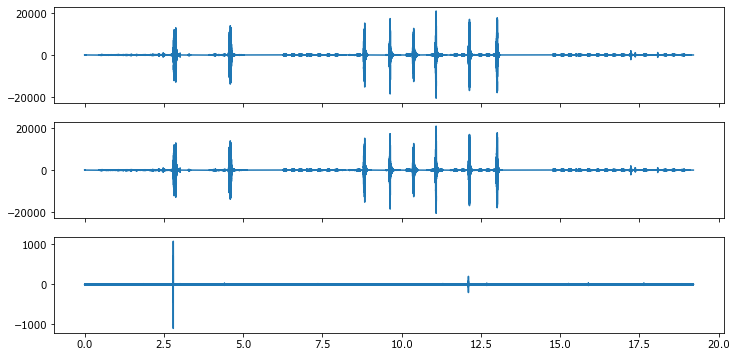
Различия между каналами незначительны и дальше мы можем работать или с одним каналом, или с их средним.
y = y[:,0]
y.shape
(846848,)
Визуально выделяются несколько частей - два звука с интервалом около 2 с, 6 звуков с интервалом около 1 с и еще более тихие звуки - шум.
Можно заметить, что после громких звуков шум меньше по амплитуде - это отражение динамической подстройки чувствительности микрофона при записи: когда громких звуков нет - чувствительность растет до определенного уровня.
Давайте послушаем шум. Чтобы получить позицию в массиве данных, соответствующую заданной секунде, нужно время умножить на частоту (rate, frequency). Поскольку позиция (index) не может быть дробным числом, то преобразовываем его в целое (integer).
int(6.1*fs)
269010
shum = y[int(6*fs):int(8.2*fs)]
plot(shum);
Audio(shum, rate=fs, autoplay=True)
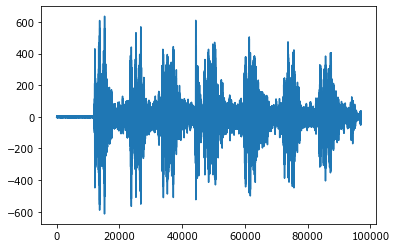
По контуру можно различить шесть однотипных звуков, убывающих по интенсивности. Перед 4-м звуком еще один короткий резкий звук.
В зависимости от того, что мы хотим изучать - полезным сигналом и шумом можно считать разные компоненты звука.
Даже там, где на графике ничего не заметно - звук есть. Даже при записи полной тишины присутствуют помехи оборудования.
shum = y[230000:274000]
plot(shum);
Audio(shum, rate=fs, autoplay=True)
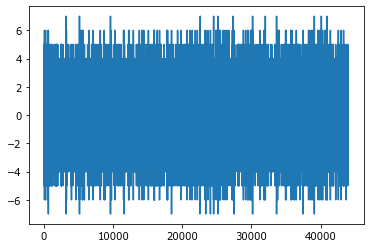
Давайте выберем секунду записи с самым громким звуком. Чтобы получить целое число для позиций, отстоящих на полсекунды до и после события, мы делим частоту на два, но при делении используем двойной знак деления.
fs/2, fs//2
(22050.0, 22050)
i = argmax(y)
signal = y[i-fs//2:i+fs//2]
plot(signal);
title('max(y) = {} у.е.'.format(max(y)));
Audio(signal, rate=fs, autoplay=True)
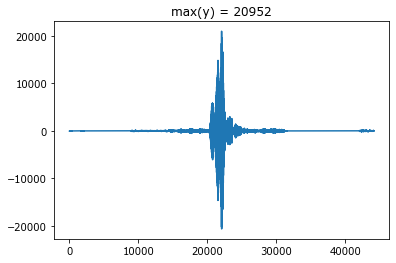
Если обратить внимание на ось ординат на нескольких последних рисунках, то видно, что амплитуда шума составляет около 6 у.е., а фоновых звуков около 600 у.е., что намного меньше максимальной амплитуды сигнала - свыше 20000 у.е. Громкость цифрового звука измеряется в у.е. и реально задается регулятором громкости колонок или наушников. Громкость реальных звуков измеряют в дБ - относительно порога слышимости.
max(y)/array([6, 600])
array([3492. , 34.92])
1 дБ означает увеличение звукового давления в \(10^{0.05}\) ≈ 1.122 раза. Относительная громкость в дБ расcчитывается по формуле: $\( B = 20 \ lg_{10}\frac{F_1}{F_0}\)$
20*log10(_)
array([70.8614847, 30.8614847])
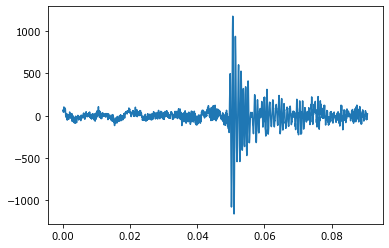
Интересный звук находится на 18-й секунде записи. Он очень короткий, поэтому частотная составляющая не воспринимается. Звук при одномоментном резком перепаде интенсивности (давления воздуха) называется щелчок.
shum = y[795000:799000]
plot(arange(len(shum))/fs, shum);
Audio(shum, rate=fs, autoplay=True)
specgram(shum, Fs=fs);
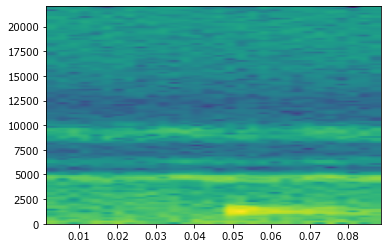
На спектрограмме видно, что наиболее выраженный сигнал, начинающийся с момента щелчка, имеет частоту около 1 кГц.
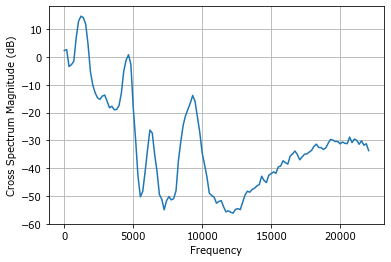
Для более точного определения частоты используют периодограммы, или в просторечии «спектр». На выходе мы получаем суммарную оценку спектральной плотности сигнала: как бы сжимаем спектрограмму по вертикали и кладем ее на бок. Рисунок по-умолчанию отображается в логарифмической шкале, дБ.
P, ff = csd(shum, shum, Fs=fs, scale_by_freq=True);
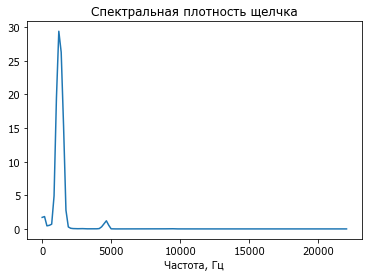
В обычной шкале наибольший пик значительно выше остальных.
plot(ff,P); title('Спектральная плотность щелчка'); xlabel('Частота, Гц');
Значения спектральной плотности в виде комплексных чисел. Можно перевести их в дБ как на предыдущем рисунке.
vv = 10*log10(real(P))
plot(ff,vv); title('Спектральная плотность щелчка'); xlabel('Частота, Гц'); ylabel('Спектральная плотность, дБ');
grid();
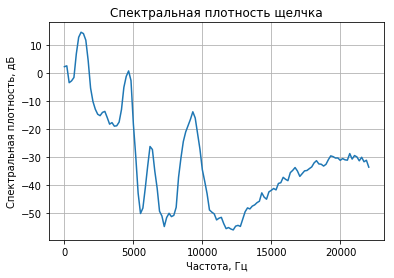
Чтобы получить частоту щелчка, нужно найти индекс максимума на этом графике, и получить значение частоты с этим же индексом. Точность зависит от параметров сглаживания при расчете спектра.
ff[argmax(vv)]
1205.859375
Для автоматического выделения отдельных звуков существуют специальные библиотеки. Для понимания принципов воспользуемся инструментами, доступными в базовом пакете scipy.
Аналитический сигнал - это сигнал, разложенный с помощью преобразования Гильберта. Из него мы можем выделить:
Амплитудную составляющую (отклонение на комплексной плоскости) - огибающую (envelope), которая отражает выраженность сигнала.
Частотную составляющую (угол движения на комплексной плоскости) - мгновенную частоту.
analytic_signal = hilbert(shum)
amplitude_envelope = np.abs(analytic_signal)
instantaneous_phase = np.unwrap(np.angle(analytic_signal))
instantaneous_frequency = np.diff(instantaneous_phase) / (2.0*np.pi) * fs
fig, (ax0, ax1) = subplots(2,1, figsize=(12,6), sharex=True)
ax0.plot(shum, label='signal')
ax0.plot(amplitude_envelope, label='envelope')
ax0.legend()
ax1.plot(instantaneous_frequency)
ylim(0, 2000);
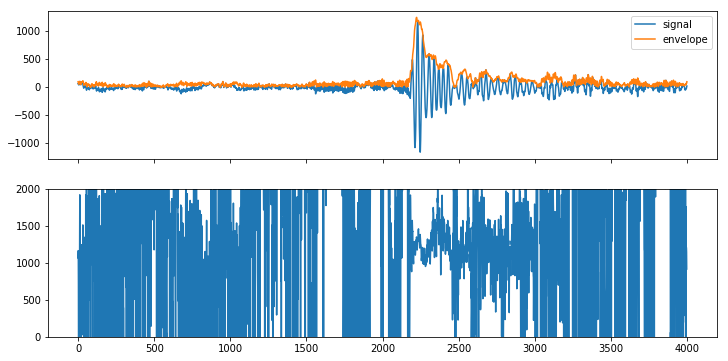
График мгновенной частоты сильно колеблется и лишь в районе звука концентрируется между 1000 и 1500 Гц. Любые шероховатости графика можно сгладить фильтром. Попробуем сгладить график мгновенной частоты, чтобы понять как она изменялась на этом промежутке.
@interact(win=(11,1001,10), order=(1,3))
def smooth(win=301, order=1):
plot(savgol_filter(instantaneous_frequency, win, order))
vlines([2200, 3200], 0, 4000, color='r', linestyles=':')
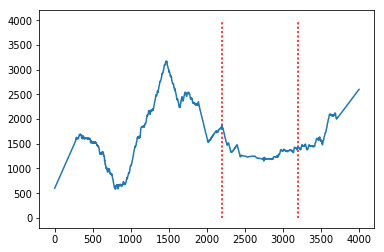
Видно, что мгновенная частота в районе щелчка составляет примерно 1200. Поскольку при сглаживании мы все равно усредняли, то оценка частоты сигнала по спектру или спектрограмме более точная и удобная.
Амплитудная составляющая - огибающая - после сглаживания может быть полезна для выделения отдельных звуков.
og = savgol_filter(amplitude_envelope, 125, 2)
plot(shum, label='сигнал')
plot(og, 'r', label='огибающая')
legend();
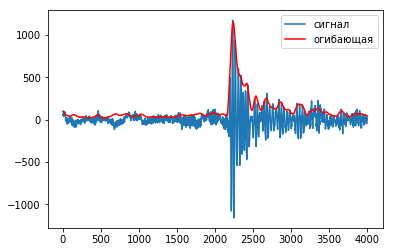
Повторим успех на всей записи.
def ogibai(y):
return savgol_filter(np.abs(hilbert(y)), 325, 2)
og=ogibai(y);
fig, ax = subplots(1,1, figsize=(12,3), sharex=True)
x = arange(len(y))/fs
plot(x,y);
plot(x,og,'r');
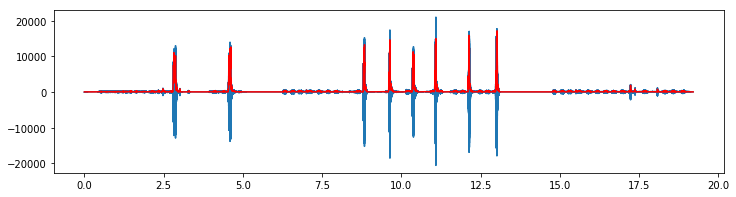
Зададим порог вполовину от максимума, или меньше, и выделим все участки сигнала превышающие порог.
Рассмотрим подробнее первый найденный участок с сигналом.
porog=1000
bb = og>porog
i1 = argmax(bb)
k=3 #множитель для наглядности
figsize(12,3);
ii = slice(i1-5000, i1+8000)
plot(x[ii], k*og[ii]/max(og), label='огибающая');
plot(x[ii], bb[ii], label='индикатор');
axhline(k*porog/max(og), color='r', label='порог');
legend();
# ylim(0,2);
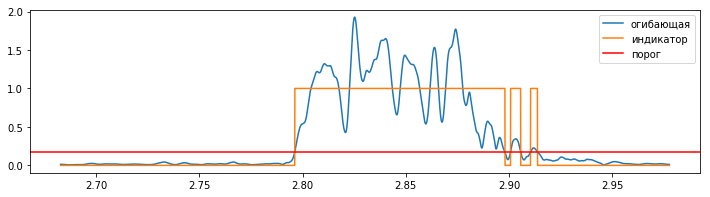
С помощью критерия мы получили квазисигнал, который равен 1 там, где исходный сигнал выше порога и 0, где - ниже.
Можно воспринимать этот квазисигнал как индикатор двух состояний: есть сигнал / нет сигнала.
Возможны три варианта перехода между состояниями (в скобах разница между соседними точками):
состояние не изменилось (0).
появился сигнал (+1).
исчез сигнал (-1).
В околопороговых зонах бывают краевые эффекты - неустойчивые колебания состояния при переключении - в электротехнике называется дребезг.
Найдем точки смены состояний.
iiab = find(diff(bb.astype(int))==1)+1
iiad = find(diff(bb.astype(int))==-1)+1
#число точек смены состояний должно совпасть!
iiab, iiad
(array([123314, 127922, 128348, 200430, 204541, 204868, 387855, 390900,
391334, 423404, 424122, 425678, 426238, 426990, 427489, 456173,
456992, 459171, 459913, 487345, 488010, 490090, 490981, 533790,
534388, 536487, 537083, 572172, 572927, 574798, 575429, 575980,
759737], dtype=int64),
array([127802, 128137, 128496, 204410, 204766, 205205, 390557, 391253,
391727, 424038, 425651, 426001, 426533, 427155, 427573, 456923,
458980, 459761, 460054, 487903, 490039, 490566, 491083, 534310,
536365, 536988, 537147, 572858, 574705, 575171, 575583, 576086,
759916], dtype=int64))
Если между окончанием одного сигнала и началом следующего очень маленький промежуток (например, 0.2 с), то их объединяем.
isi = iiad[1:]-iiab[:-1]
hist(isi, 40);

Найдем индексы всех точек смены состояния, находящихся близко друг к другу, и удалим их.
ii_drebezg = find(isi < fs//5)
iiab = delete(iiab ,ii_drebezg+1)
iiad = delete(iiad ,ii_drebezg)
plot(og, label='огибающая');
vlines(iiab, 0, 20000, color='r', label='начало')
vlines(iiad, 0, 20000, color='m', label='конец')
legend();
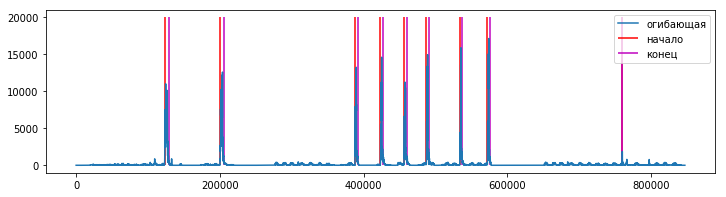
После определения положения всех обособленных звуков можно анализировать каждый из них индивидуально и сравнивать между собой.
dd = (iiad-iiab)/fs * 1000
isi = diff(iiab+dd)/fs #между центрами звуков
#этой конструкцией мы делим сигнал на фрагменты по всем найденным индексам и считаем максимум в каждом втором
a = [max(_x) for i,_x in enumerate(split(og, sort(hstack([iiab,iiad])))) if i%2]
figsize(12,3);
subplot(131)
bar(arange(len(dd)), dd); title('Длительность звуков, мс');
subplot(132)
bar(arange(len(isi)), isi); title('Интервал между звуками, с');
subplot(133)
bar(arange(len(a)), a); title('Громкость, у.е.');
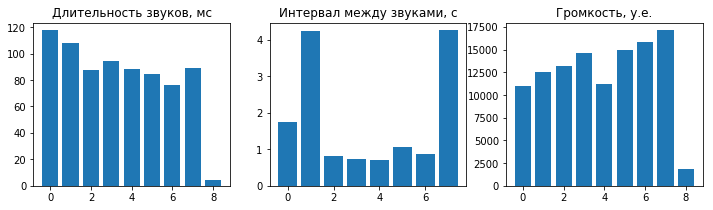
Можно отобрать интересующие нас звуки для анализа, оформить результаты в виде готового набора данных и т.д.
figsize(10,5)
for iab,iad in zip(iiab,iiad):
y1 = y[iab:iad]
P, ff = csd(y1, y1, NFFT=1000, Fs=fs);
legend(arange(len(iiab))+1);
xlim(0,4000);
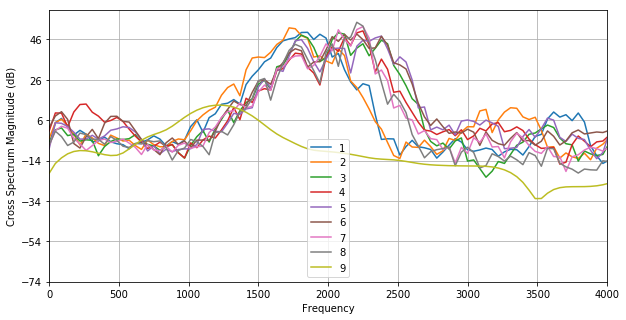
На спектре видно несколько частотных пиков: 1800, 2100, 2200 Гц.
Спектральная плотность для 1 и 2 звуков ниже, чем для остальных. В 3-, 5- и 6-м звуках есть более высокие второстепенные тоны с частой свыше 2400 Гц.
Более детальная структура звука определяет его тембр. Идеи дальнейшего анализа отдельных звуковых формантов могут появиться при анализе спектрограмм. Построим спектрограмму каждого из 8 звуков длительностью около 100 мс.
fig, axx = subplots(1,8, sharex=True, sharey=True, figsize=(14,3), subplot_kw=dict(xticks=[0.05,0.1]))
for i,iab in enumerate(iiab[:8]):
axes(axx[i])
specgram(y[iab-fs//40:iab+5600], NFFT=1000, Fs=fs, noverlap=0)
ylim(0,10000)
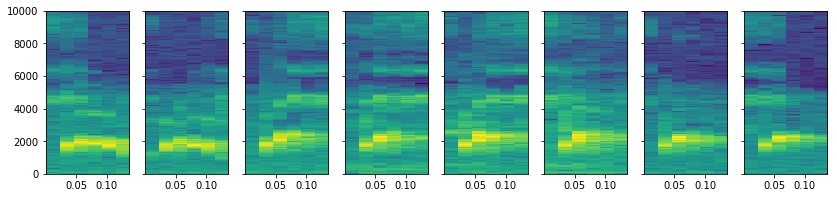
На спектрограммах видно, что частотный пик первых двух звуков стабильный, а у остальных шести - повышается. Также у звуков с третьего по пятый заметна обертоника в районе 4000 Гц, которая звучит вместе с частотой 6500 Гц. Эти частотные пики мы уже видели на спектре мощности всей звукозаписи. Сравнение спектрограмм позволяет оценить спектральную неоднородность отдельных звуков и выявить динамическую смену частотного состава.
