Частоты кодонов
Содержание
Частоты кодонов¶
Одна из проблем при исследовании экспрессии белков связана с редкими кодонами в кодирующей последовательности. Рассмотрим частоты встречаемости (на 1000) кодонов в генах различных организмов.
Примечание
Отношение 1 к 100 называется «pro cent» (лат. к сотне), в русском языке слово «процент» склоняют во всех падежах. А отношение 1 к 1000 - «pro mille» (лат. к тысяче). Это слово не склоняют.
знак |
русский |
латынь |
английский |
|---|---|---|---|
% |
процент |
per centum |
percent |
‰ |
промилле |
per mille |
permille |
Представленные данные взяты из «Codon-Usage Database» содержащей 392382 полных кодирующих последовательностей для 11713 организмов. [NGI00] В таблице отобраны 7 видов со следующими обозначениями.
spec=dict([_s.strip().split(' ',1) for _s in '''
HUM Homo sapiens
MUS Mus musculus
DRO Drosophila melanogaster
ATH Arabidopsis thaliana
YSC Saccharomyces cerevisiae
PIC Pichia pastoris
ECO Escherichia coli
'''.strip().split('\n')])
spec
{'HUM': 'Homo sapiens',
'MUS': 'Mus musculus',
'DRO': 'Drosophila melanogaster',
'ATH': 'Arabidopsis thaliana',
'YSC': 'Saccharomyces cerevisiae',
'PIC': 'Pichia pastoris',
'ECO': 'Escherichia coli'}
Понимание смещения в частоте встречаемости кодонов занимает центральное место в таких областях, как молекулярная эволюция и биотехнология [PK11].
Скопируем текст таблицы, в которой представлены промилле кодонов с указанием аминокислоты у этих видов.
s='''Am Codon HUM MUS DRO ATH YSC PIC ECO
Arg CGA 6.2 6.6 8.5 6.3 3.0 4.4 4.1
Arg CGC 10.6 9.5 18.1 3.8 2.6 2.2 18.3
Arg CGG 11.5 10.4 8.2 4.9 1.8 2.0 6.5
Arg CGU 4.6 4.7 8.8 9.0 6.4 6.8 18.8
Arg AGA 11.9 11.6 5.2 18.9 21.3 20.2 4.5
Arg AGG 11.9 11.9 6.3 10.9 9.3 6.6 2.6
Leu CUA 7.1 7.9 8.2 9.9 13.4 10.9 4.5
Leu CUC 19.7 20.2 13.8 16.1 5.4 7.5 10.1
Leu CUG 39.9 39.9 38.3 9.8 10.5 15.1 45.8
Leu CUU 13.1 13.2 8.9 24.1 12.3 15.7 12.6
Leu UUA 7.6 6.5 4.4 12.7 26.2 15.6 15.0
Leu UUG 12.8 13.3 16.1 20.9 27.1 31.2 12.9
Ser UCA 12.2 11.6 7.8 18.2 18.7 15.4 10.0
Ser UCC 17.7 18.0 19.5 11.2 14.2 16.2 9.3
Ser UCG 4.5 4.3 16.7 9.3 8.6 7.1 8.5
Ser UCU 15.1 16.0 7.0 25.1 23.4 23.9 11.0
Ser AGC 19.4 19.6 20.5 11.3 9.7 7.7 15.0
Ser AGU 12.1 12.5 11.5 14.0 14.2 12.8 10.8
Thr ACA 15.0 15.8 11.1 15.7 17.8 13.7 10.8
Thr ACC 19.0 19.1 21.3 10.3 12.6 14.3 21.3
Thr ACG 6.1 5.8 14.5 7.7 8.0 6.0 13.8
Thr ACU 13.0 13.6 9.5 17.6 20.2 22.3 11.0
Pro CCA 16.9 17.1 13.5 16.1 18.1 18.4 8.7
Pro CCC 19.9 18.3 18.0 5.3 6.8 6.7 5.6
Pro CCG 7.0 6.2 16.0 8.6 5.3 4.2 19.3
Pro CCU 17.5 18.4 6.9 18.7 13.5 16.0 8.0
Ala GCA 15.9 15.9 12.8 17.5 16.2 15.0 21.6
Ala GCC 28.0 26.4 33.6 10.4 12.6 16.5 23.8
Ala GCG 7.5 6.6 14.1 9.0 6.2 3.8 27.9
Ala GCU 18.5 20.2 14.4 28.4 21.1 29.0 17.4
Gly GGA 16.4 16.8 17.7 24.2 10.9 19.1 10.7
Gly GGC 22.4 21.6 26.6 9.2 9.8 8.0 25.5
Gly GGG 16.5 15.3 4.7 10.2 6.0 5.8 11.6
Gly GGU 10.8 11.5 13.2 22.3 23.8 26.0 24.9
Val GUA 7.1 7.4 6.4 9.9 11.8 9.8 12.0
Val GUC 14.6 15.5 13.9 12.8 11.6 14.8 14.0
Val GUG 28.3 28.9 27.8 17.4 10.8 12.2 23.4
Val GUU 11.0 10.6 10.9 27.3 22.0 27.1 20.1
Lys AAA 24.2 21.7 16.8 30.8 42.0 30.4 35.6
Lys AAG 32.0 34.1 39.6 32.7 30.8 34.7 13.1
Asn AAC 19.1 20.6 26.3 20.9 24.8 26.1 21.1
Asn AAU 16.8 15.5 21.1 22.3 35.8 24.6 23.0
Gln CAA 12.1 11.5 15.7 19.4 27.3 25.3 14.4
Gln CAG 34.2 34.3 36.5 15.2 12.2 16.2 28.0
His CAC 15.1 15.2 16.0 8.7 7.8 9.1 8.8
His CAU 10.8 10.3 10.6 13.7 13.7 11.9 12.5
Glu GAA 28.7 26.9 21.0 34.3 45.7 39.0 37.9
Glu GAG 39.6 39.9 42.7 32.3 19.3 29.7 18.8
Asp GAC 25.2 26.5 24.6 17.3 20.2 26.2 18.8
Asp GAU 21.7 21.2 27.5 36.7 37.7 36.0 32.9
Tyr UAC 15.3 16.3 18.3 13.8 14.7 18.2 12.0
Tyr UAU 12.1 12.1 10.8 14.7 18.8 15.2 18.4
Cys UGC 12.6 12.0 13.2 7.1 4.7 4.2 6.0
Cys UGU 10.5 11.0 5.4 10.5 8.0 7.7 5.4
Phe UUC 20.4 21.9 21.9 20.7 18.4 19.8 15.6
Phe UUU 17.4 17.0 13.2 21.8 26.2 23.6 22.6
Ile AUA 7.4 7.1 9.5 12.6 17.8 11.7 8.3
Ile AUC 20.9 22.9 22.9 18.6 17.1 19.6 22.6
Ile AUU 15.8 15.4 16.5 21.5 30.1 30.8 29.7
Met AUG 22.1 22.9 23.6 24.5 21.0 18.1 25.9
Trp UGG 13.2 12.3 9.9 12.5 10.4 10.3 13.8
Ter UAA(ochre) 1.0 0.7 0.8 0.9 1.0 0.9 2.0
Ter UAG(amber) 0.8 0.6 0.6 0.5 0.5 0.5 0.3
Ter UGA(opal) 1.6 1.2 0.5 1.1 0.7 0.3 1.0
'''
A = pd.read_csv(StringIO(s), index_col=(0,1), sep='\t')
A
| HUM | MUS | DRO | ATH | YSC | PIC | ECO | ||
|---|---|---|---|---|---|---|---|---|
| Am | Codon | |||||||
| Arg | CGA | 6.2 | 6.6 | 8.5 | 6.3 | 3.0 | 4.4 | 4.1 |
| CGC | 10.6 | 9.5 | 18.1 | 3.8 | 2.6 | 2.2 | 18.3 | |
| CGG | 11.5 | 10.4 | 8.2 | 4.9 | 1.8 | 2.0 | 6.5 | |
| CGU | 4.6 | 4.7 | 8.8 | 9.0 | 6.4 | 6.8 | 18.8 | |
| AGA | 11.9 | 11.6 | 5.2 | 18.9 | 21.3 | 20.2 | 4.5 | |
| ... | ... | ... | ... | ... | ... | ... | ... | ... |
| Met | AUG | 22.1 | 22.9 | 23.6 | 24.5 | 21.0 | 18.1 | 25.9 |
| Trp | UGG | 13.2 | 12.3 | 9.9 | 12.5 | 10.4 | 10.3 | 13.8 |
| Ter | UAA(ochre) | 1.0 | 0.7 | 0.8 | 0.9 | 1.0 | 0.9 | 2.0 |
| UAG(amber) | 0.8 | 0.6 | 0.6 | 0.5 | 0.5 | 0.5 | 0.3 | |
| UGA(opal) | 1.6 | 1.2 | 0.5 | 1.1 | 0.7 | 0.3 | 1.0 |
64 rows × 7 columns
Возможных комбинаций кодонов \( 4 ^ 3 = 64\), 3 - терминальные. Оценка равной вероятности на 1000 кодонов:
p0=1000/61
p0
16.39344262295082
Таким образом, если бы распределение было равномерным, то частота для всех кодирующих кодонов была бы в районе 16.4.
Для визуализации частот выберем часть кодонов: которые кодируют аргинин и серин, аминокислоты с шестикратной вырожденностью.
A.loc['Arg'].plot(kind='pie', subplots=True, figsize=(10, 5), legend=False, labels=None, layout=[2,4]);
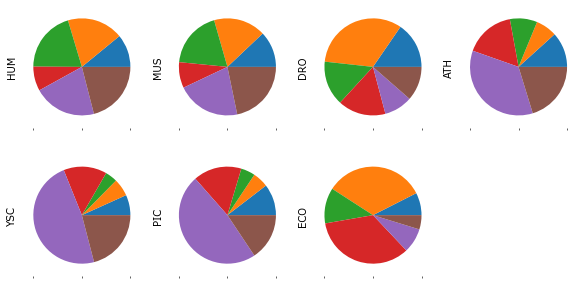
A.loc['Ser'].plot(kind='pie', subplots=True, figsize=(10, 5), legend=False, labels=None, layout=[2,4]);
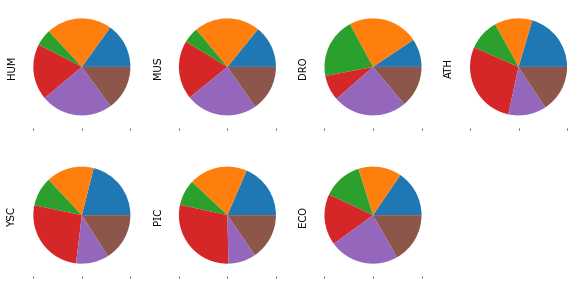
Распределения кодонов для аргинина заметно различаются, а для серина более или менее равномерны. При этом доля конкретной аминокислоты в белках примерно одинаковая у всех живых организмов.
A.loc['Arg'].T.plot(kind='bar', stacked=1);
legend(loc='center left', bbox_to_anchor=(1.0, 0.5));
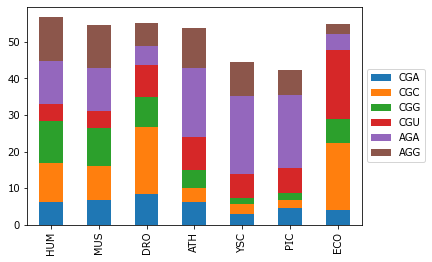
Обратите внимание, что для вынесения легенды за пределы рисунка мы используем специальную команду с указанием координат размещения рамки для легенды.
Посмотрите распределение кодонов для других аминокислот. Для каких из них есть существенные различия в частотах?
A.index.levels[0]
Index(['Ala', 'Arg', 'Asn', 'Asp', 'Cys', 'Gln', 'Glu', 'Gly', 'His', 'Ile',
'Leu', 'Lys', 'Met', 'Phe', 'Pro', 'Ser', 'Ter', 'Thr', 'Trp', 'Tyr',
'Val'],
dtype='object', name='Am')
В таблице двухуровневый индекс. Первый уровень 'Am' представлен списком аминокислот, второй 'Codon' - списком кодонов. Позиция в таблице определяется сочетанием значений из первого и второго индекса.
Для отбора по многоуровнему индексу можно использовать метод .query() указывая нужный уровень индекса по имени.
A.query('Codon in ("AGA","AGG","AGC","AGU")')
| HUM | MUS | DRO | ATH | YSC | PIC | ECO | ||
|---|---|---|---|---|---|---|---|---|
| Am | Codon | |||||||
| Arg | AGA | 11.9 | 11.6 | 5.2 | 18.9 | 21.3 | 20.2 | 4.5 |
| AGG | 11.9 | 11.9 | 6.3 | 10.9 | 9.3 | 6.6 | 2.6 | |
| Ser | AGC | 19.4 | 19.6 | 20.5 | 11.3 | 9.7 | 7.7 | 15.0 |
| AGU | 12.1 | 12.5 | 11.5 | 14.0 | 14.2 | 12.8 | 10.8 |
Отображение на основе частотных распределений¶
A.plot(kind='density');
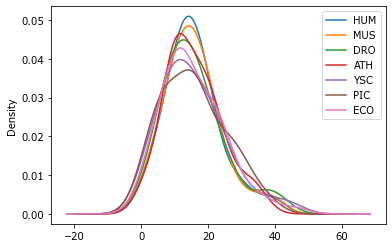
Типичные значения частоты кодонов в районе 15 промилле.
Распределение похоже на нормальное. Мы можем применить сингулярное разложение для извлечения главных компонент.
A = A-p0
U,sigma,V = svd(A, full_matrices=False)
sigma
array([155.90509657, 88.38299524, 52.52879423, 29.80419437,
24.89140322, 16.69400044, 3.97487486])
bar(arange(len(sigma)),sigma);
ylabel('Вклад компонента');
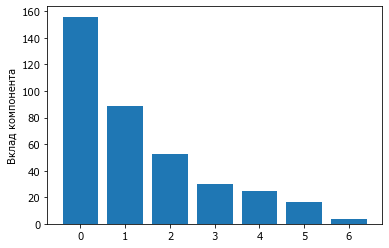
figure(figsize=[10,4])
subplot(121); pcolor(U);
subplot(122); pcolor(V.T);
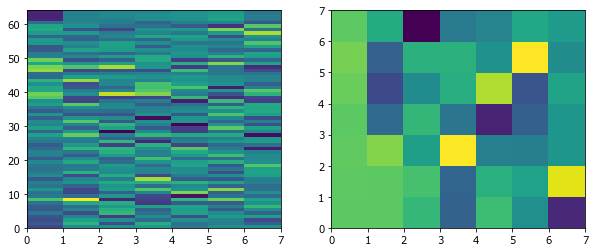
Выберем несколько первых компонентов и посчитаем долю вариации, которую они вместе объясняют.
nF=3
W=diag(sigma)
Q = dot(W[:nF,:nF],V[:nF,:]);
B = dot(U[:,:nF], Q);
sum(sigma[:nF]**2)/sum(sigma**2)
0.9508620103515191
subplot(121); pcolor(A); subplot(122); pcolor(B);
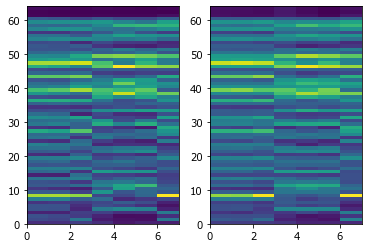
Слева - исходная матрица, справа - восстановленная по трём главным компонентам.
Первые два компонента часто используют для отображения на плоскости (ембеддинга).
fig,ax = subplots(figsize=(8,5))
i1,i2=0,1
ax.scatter(Q[i1,:],Q[i2,:]);
[text(Q[i1,i], Q[i2,i]+0.5, spec[_s]) for i,_s in enumerate(spec)];
xlabel('Factor 1'); ylabel('Factor 2');

Можно сделать ембеддинг и по трем компонентам, но объемные картинки сложнее для восприятия.
from mpl_toolkits.mplot3d.axes3d import Axes3D
figure(figsize=(12,8))
ax=subplot(111, projection='3d')
ax.scatter(Q[1,:],Q[2,:],Q[0,:])
ax.view_init(20, 35)
# добавим подписи к некоторым точкам
for i in [0, 1, 5, 6]:
ax.text(Q[1,i],Q[2,i],Q[0,i],spec[A.columns[i]])
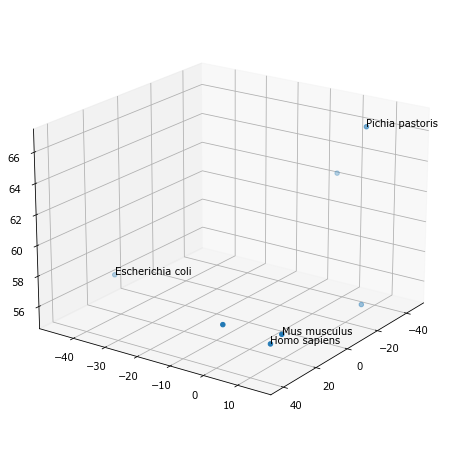
Если по двум первым факторам кишечная палочка (E. coli) была близка к млекопитающим, то в трехмерном отображении она удалилась, и картина в целом стала больше соответствовать эволюционной дистанции между видами.
